Combining human governance with mechanisms, the second phase of L2 is more resilient to fragility.

Written by: Vitalik Buterin

Translated by: Wenser, Odaily Planet Daily

Editor's Note: The discussion about the three phases of Ethereum rollup security has always been a focal point for the Ethereum ecosystem community. This is not only related to the operational stability of the Ethereum mainnet and L2 networks but also concerns the real development status of L2 networks. Recently, Ethereum community member Daniel Wang proposed the naming label #BattleTested for the L2 network Stage 2 on the X platform, arguing that only L2 networks with current code and configurations that have been live on the Ethereum mainnet for over 6 months, maintaining a total locked value (TVL) of over $100 million, with at least $50 million in ETH and major stablecoins, can earn this title. This title is dynamically assessed to avoid the emergence of "on-chain phantoms." Ethereum co-founder Vitalik subsequently provided a detailed explanation and shared his views on the issue, which Odaily Planet Daily has translated as follows.

The Three Phases of L2 Networks: From 0 to 1 to 2, Security Determined by Governance Shares

The three phases of Ethereum rollup security can be determined based on when the security council can cover the trustless (i.e., purely cryptographic or game-theoretic) components:

• Phase 0: The security council has complete control. There may be a functioning proof system (Optimism or ZK mode), but the security council can overturn it through a simple majority vote. Therefore, the proof system is merely "consultative."

• Phase 1: The security council needs 75% (at least 6/8) approval to override the operating system. There must be a quorum to prevent a subset (e.g., ≥ 3) from acting outside the main organization. Thus, controlling the proof system is relatively difficult but not insurmountable.

• Phase 2: The security council can only act in the case of provable errors. For example, a provable error might be two redundant proof systems (e.g., OP and ZK) contradicting each other. If there is a provable error, it can only choose one of the proposed answers: it cannot arbitrarily respond to a particular mechanism.

We can represent the "voting shares" held by the security council at different stages with the following chart:

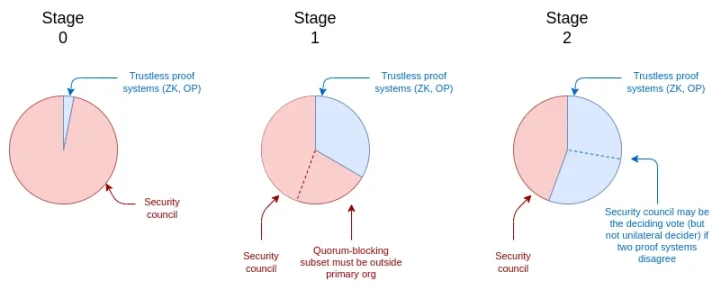
Governance Voting Structure of the Three Phases

An important question is: What are the optimal timings for the L2 network to transition from Phase 0 to Phase 1, and from Phase 1 to Phase 2?

The only valid reason for not immediately entering Phase 2 is that you cannot fully trust the proof system—this is an understandable concern: the system consists of a large amount of code, and if there are vulnerabilities in the code, attackers could steal all users' assets. The stronger your confidence in the proof system (or conversely, the weaker your confidence in the security council), the more you want to push the entire network ecosystem to advance to the next phase.

In fact, we can quantify this with a simplified mathematical model. First, let’s list the assumptions:

• Each member of the security council has a 10% chance of "individual failure";

• We treat active failures (refusal to sign contracts or key unavailability) and security failures (signing incorrect matters or keys being hacked) as equally likely events. In reality, we only assume one category of "failure," where "failed" security council members both sign incorrect matters and fail to sign the correct ones;

• In Phase 0, the security council's decision criterion is 4/7, and in Phase 1, it is 6/8;

• We assume there is a single overall proof system (as opposed to a 2/3 design mechanism, where the security council can break ties when opinions contradict). Therefore, in Phase 2, the existence of the security council is fundamentally irrelevant.

Under these assumptions, considering the specific probability of the proof system collapsing, we want to minimize the likelihood of the L2 network collapsing.

We can use a binomial distribution to accomplish this:

• If each member of the security council has a 10% chance of independent failure, then the probability that at least 4 out of 7 fail is ∑𝑖= 47( 7 𝑖)∗ 0.1 𝑖∗ 0.97 −𝑖= 0.002728, thus the integrated system in Phase 0 has a fixed failure probability of 0.2728%.

• The integration in Phase 1 can also fail if the proof system fails and the security council's verification mechanism experiences ≥ 3 failures, preventing network computation coverage (probability ∑𝑖= 38( 8 𝑖)∗ 0.1 𝑖∗ 0.98 −𝑖= 0.03809179 multiplied by the proof system failure rate), or if the security council experiences 6 or more failures, it can forcefully generate an incorrect computation answer (fixed ∑𝑖= 68( 8 𝑖)∗ 0.1 𝑖∗ 0.98 −𝑖= 0.00002341 probability);

• The probability of failure in Phase 2 is consistent with the probability of the proof system failing.

Here is the presentation in chart form:

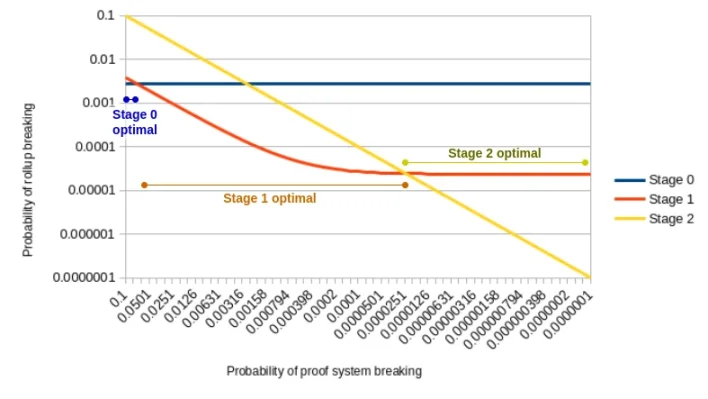
Probability of Proof System Failure at Different Stages of L2 Networks

As inferred from the results above, as the quality of the proof system improves, the optimal stage transitions from Phase 0 to Phase 1, and then from Phase 1 to Phase 2. Running a network in Phase 2 with a proof system of Phase 0 quality yields the worst outcome.

Now, note that the assumptions in the above simplified model are not perfect:

• In reality, members of the security council are not completely independent; there may be "common mode failures" among them: they may collude, or all be subject to the same coercion or hacking, etc. The requirement for a quorum to prevent a subset from acting outside the main organization aims to avoid this occurrence, but it is still not perfect.

• The proof system itself may be composed of multiple independent systems (which I have advocated in previous blogs). In this case, (i) the probability of the proof system collapsing is very low, and (ii) even in Phase 2, the security council is important because it is key to resolving disputes.

These two arguments suggest that, compared to what is shown in the chart, Phase 1 and Phase 2 are more attractive.

If you believe in the mathematics, then the existence of Phase 1 is almost never justified: you should move directly to Phase 1. The main objection I hear is that if a critical error occurs, it may be difficult to quickly obtain signatures from 6 out of 8 security council members to fix it. However, there is a simple solution: grant any one security council member the authority to delay withdrawals by 1 to 2 weeks, giving others enough time to take remedial action.

At the same time, however, jumping too early to Phase 2 is also incorrect, especially if the work transitioning to Phase 2 comes at the expense of strengthening the underlying proof system. Ideally, data providers like L2Beat should showcase proof system audits and maturity indicators (preferably metrics for the implementation of the proof system rather than the entire aggregate, so we can reuse them), along with demonstrating the phases.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。