Always feeling that one more round could turn the tide is precisely because we mistakenly equate the group average with individual fate.
Author: Xue E, DataCafe

Imagine you participate in a coin-flipping challenge game with an initial capital of 1000 yuan, and you can choose to keep playing:
Each round, you flip a coin.
If it lands heads, your wealth increases by 80%.
If it lands tails, your wealth decreases by 50%.
It sounds like a surefire game!
But the reality is…
If you let 100,000 players participate in this game and have them each play 100 rounds, you will find that their average wealth indeed grows exponentially, but the vast majority end up with less than 72 yuan, or even go bankrupt!
Why is the average wealth increasing, but most people end up poorer?
This is a typical non-ergodic trap. Always feeling that one more round could turn the tide is precisely because we mistakenly equate the group average with individual fate.
Non-ergodic Trap: Long-term Average ≠ Your True Fate
What is ergodicity?
The concept of ergodicity first appeared in statistical physics and has had a profound impact in fields such as probability theory, finance, behavioral science, and machine learning. The core question it seeks to answer is: Is the long-term average applicable to individuals? When making decisions, should we trust the 'long-term average' or the reality of 'personal experiences'?
In the 19th century, physicist Ludwig Boltzmann proposed the ergodic hypothesis while studying the motion of gas molecules: If you observe a gas molecule long enough, it will traverse all possible states.
Imagine a closed gas container filled with countless gas molecules, each experiencing different velocity trajectories during collisions. The long-term trajectory of a single molecule is the same as the statistical distribution of the entire gas, meaning we can use the state of all molecules at a certain moment to infer the long-term trajectory of a single molecule.
This is the famous Boltzmann ergodic hypothesis.

Mathematically, ergodicity means:
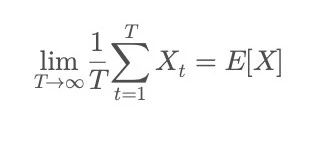
The left side represents time average: describing the average result obtained by an individual after experiencing the same process multiple times over a sufficiently long time;
The right side represents group average: describing the statistical expectation obtained by observing countless individuals at a certain moment. In other words: when the system meets the conditions of ergodicity, the performance of a single individual will eventually converge to the group's "long-term average."
If the world is ergodic, everyone's wealth will eventually approach the average wealth level of society. In an ergodic world, everyone can experience all possible economic states (wealthy, poor, successful, failed), and individual fates will always converge to the group's "long-term average."
But real life is often non-ergodic: individual resources are limited, and often one is eliminated due to a failure before experiencing all possible paths.
We often hear guiding statements like:
"The average annual income in a certain industry exceeds one million."
"Someone achieved financial freedom by 30, and it only took two years to start a business."
"A certain index fund has a high long-term annualized return; just keep investing, and you'll get rich."
…
These seemingly reasonable statistics seem to tell us a definitive truth. It seems that as long as we take action, the long-term average return will apply to individuals. But these cases belong to path-dependent and non-replicable non-ergodic processes. Imitators cannot experience the same historical context, relational networks, luck nodes, and may not even know the number of hidden failures.
Data tells you the long-term average of the group, but reality is filled with short-term "cliff-like failures."
This is the most insidious trap of non-ergodicity — the average value of big data statistics ≠ the true fate of individuals.
A single collapse may be irreparable for an individual; a single failure may completely eliminate someone, making it impossible to return to the "average state." Each person's life path can only be experienced once, and cannot, like in a casino, benefit from the group's long-term average, waiting for probabilities to average out among countless gamblers.
Why is the long-term fate of individuals often worse than the "average value"?
In non-ergodic systems, individual long-term performance is often below the group average. This is not coincidental but a systemic structural characteristic. The shiny average is often pulled up by a very small number of success stories in entrepreneurship, investment windfalls, and comebacks, while the failures of many have never entered the statistics.
In most cases, real systems are multiplicative and have path dependence characteristics — for example, the compounding of investments, the decline of health, and the destruction of reputation. The typical feature of such systems is: limited upside, unlimited downside.
A single bankruptcy can ruin a lifetime;
A single wrong decision can completely change one's fate;
A single breach of trust can completely destroy trust;
Yet the wealth that can be earned, the performance that can be increased, and the advantages that can be established are always limited.
This is why, mathematically, the long-term growth rate of multiplicative processes does not equal "average return," but is closer to:
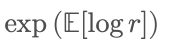
In contrast, the group average is usually represented by the arithmetic mean,
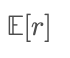
And since the logarithmic function is a strictly concave function, based on Jensen's inequality, we have:
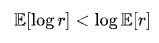
Therefore, the long-term growth rate of multiplicative systems (i.e., geometric mean) is always less than the arithmetic mean. The greater the volatility, the more pronounced this gap becomes. The arithmetic mean tells you 'what would happen if you were always lucky,' while the geometric mean tells you 'how much you have left after weathering the storms of the real world.'
This means that the long-term performance of individuals is always far below the "group average return," not due to bad luck but due to structural reasons.
How to Make Optimal Decisions? The Golden Ratio of the Kelly Criterion
So what can we do in life decisions to avoid the fate of going to zero in a long-term game? How to not go bankrupt while achieving long-term compounding?
The answer is: Never go all in, learn to bet according to the Kelly Criterion!
The Kelly Criterion is an optimal betting strategy used in repeated games, aimed at maximizing long-term returns while avoiding short-term losses that lead to elimination. It was originally proposed by John L. Kelly Jr. in 1956 at Bell Labs, intended to solve the problem of "how to allocate signal power in a noisy channel" to maximize information transmission efficiency.
Later, this theory quickly crossed over into other fields.
American mathematician and investment genius Edward Thorp discovered that the Kelly Criterion could optimize wealth growth paths. He brought the Kelly strategy to casinos and systematically defeated the blackjack dealer in "Beat the Dealer," and later took it to Wall Street in "Beat the Market" to continue "harvesting."
This criterion is essentially equivalent to maximizing logarithmic expected returns (log-utility), thus balancing growth and risk dynamically. It helps you find an optimal balance between "living long" and "earning enough."
The Kelly Criterion:
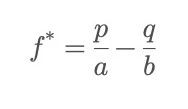
Where p is the probability of success, q = 1-p is the probability of failure; b is the return multiplier when successful (excluding the principal), and a is the loss ratio when failing (usually 1, if losing the entire bet amount).
Returning to the coin-flipping game mentioned at the beginning, you can choose to bet a certain percentage of your capital and keep playing, but how much should you bet each time?
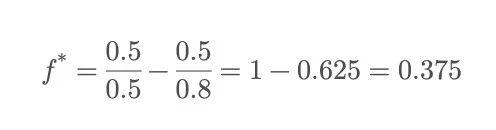
In other words, the Kelly Criterion suggests you should invest 37.5% of your total capital each time. Betting too much, even with an advantage, could lead to a total loss after a few consecutive losses; betting too little means missing out on the growth that should have been yours.
The significance of the Kelly Criterion lies in: finding that point where you can earn the most in the long run while still surviving.
To add, the Kelly Criterion is very sensitive to the odds of winning, but in reality, these parameters are often uncertain or dynamically changing, so many prudent practitioners choose to bet half of the Kelly suggested value (known as the half-Kelly strategy) to achieve a smoother return path.
Simulation Experiment: In a Coin-Flipping Game with 100,000 Players, How Many Can "Survive"?
To more intuitively understand the impact of different betting strategies on individual fate, I simulated 100,000 players participating in the aforementioned coin-flipping game, playing a total of 200 rounds, with each person playing independently.
The game rules remain: starting capital of 1000, earning 80% on heads, losing 50% on tails. Players can choose a fixed betting ratio: for example, betting all (100%), betting 65%, 37.5%, etc.
The results… Players betting 100% almost all went extinct!
The final wealth distribution showed a "power-law distribution," with a very small number of people becoming wealthy, but the vast majority of players went bankrupt.
We compared the wealth distribution of players using these four different betting strategies, with the further right the asset distribution, the higher the player's assets.
a. 100% Betting: Almost Everyone Goes Bankrupt
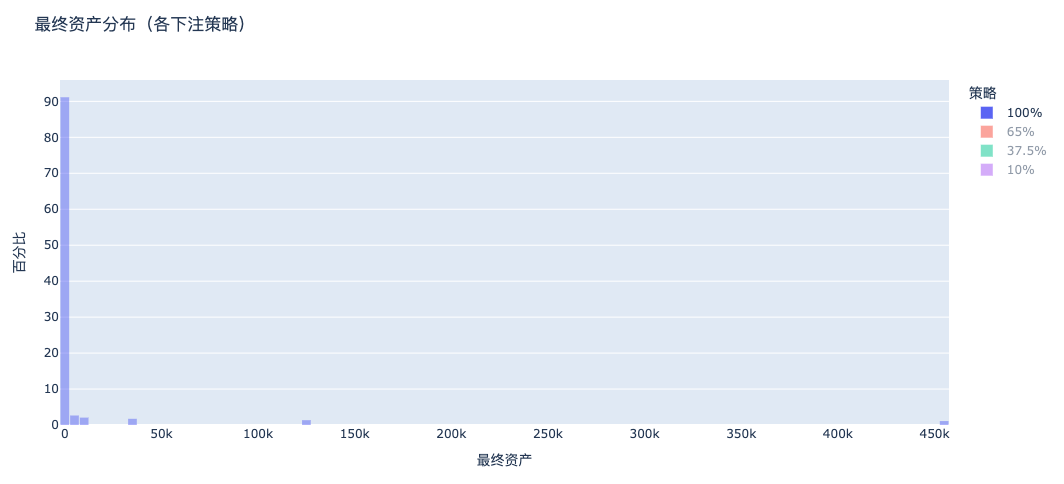
The final asset distribution under an all-in strategy has a massive left-side poverty peak + a very thin right-side wealth tail structure: most people go bankrupt, while a very small number of people take all the money, which is the true representation of game asymmetry + survivor bias.
b. 65% Betting: Still Polarized, Many Still Go Bankrupt
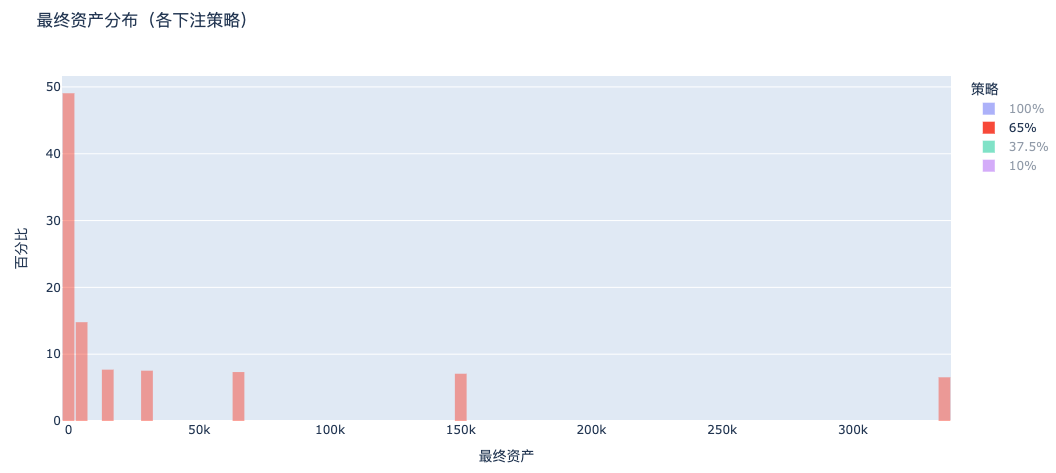
c. 37.5% Betting (Kelly Criterion): Stable Wealth Growth
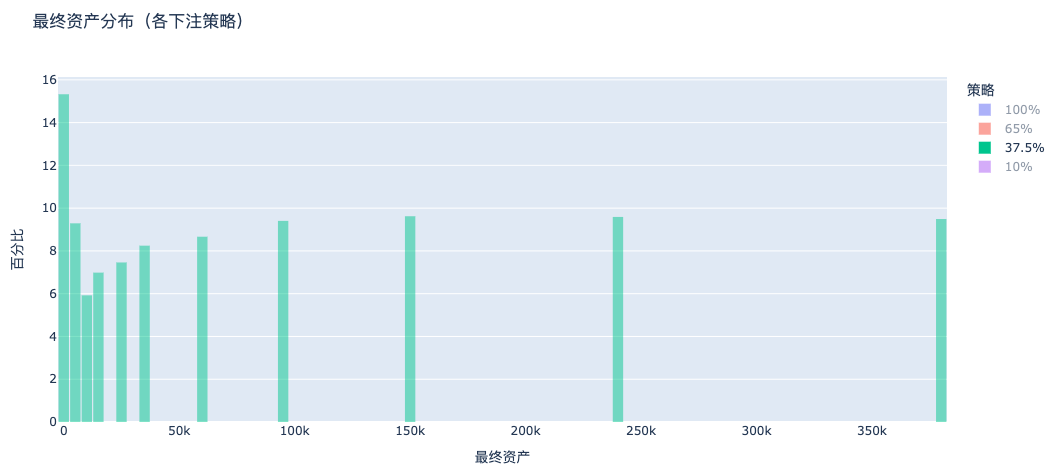
Under the Kelly betting strategy, the asset distribution shifts significantly to the right, with most people's assets increasing and the distribution becoming concentrated, representing the optimal wealth accumulation model.
d. 10% Betting: Almost No One Goes Bankrupt but Returns Are Too Low
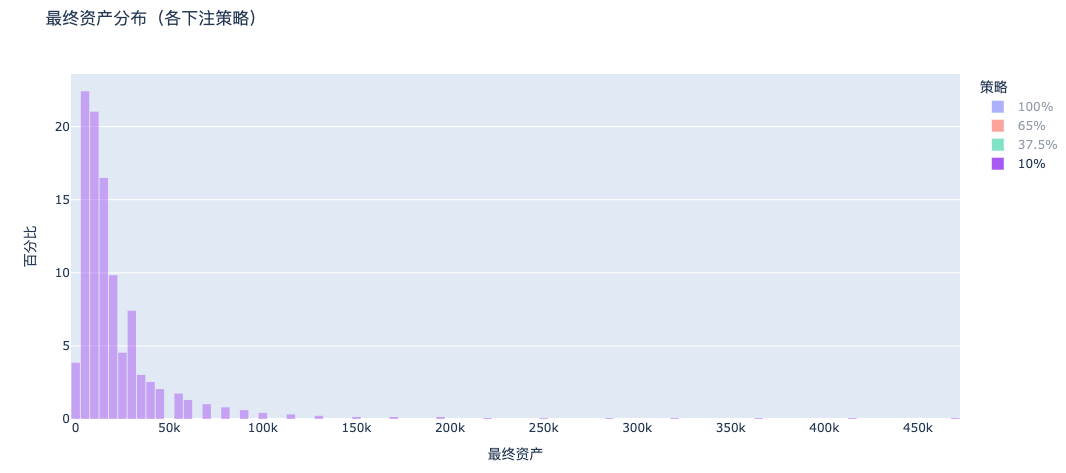
There is no peak in the bankruptcy distribution as seen in the all-in scenario, but overall wealth is concentrated in the low asset range. In contrast, the 37.5% strategy creates a noticeable long tail on the right side, achieving asset multiplication.
The Kelly betting strategy is the only one that balances "not going bankrupt in most cases" and "considerable appreciation," making it the mathematically optimal long-term survival strategy. This is the essence of the Kelly Criterion: it is not about winning the most, but ensuring you can last long enough.
The Philosophy of Life in the Kelly Criterion
The Kelly Criterion teaches us that the secret to long-term success is learning to control the proportion of "bets." Life is not about who can land a critical hit once, but about who can keep playing.
In your career, it’s not about impulsively quitting your job out of passion, nor is it about clinging to your comfort zone; it’s about continuous planning, enhancing your skills, daring to change paths, and keeping options open;
In investing, it’s not about going all in for quick riches, but about controlling your position based on odds and retaining your chips;
In relationships, it’s not about placing all your emotions and values on one person, but about investing while maintaining your individuality;
In growth and self-discipline, it’s not about relying on a single breakthrough for change, but about steadily and compoundingly optimizing your life structure.
Life is like a long game; your goal is not to win once, but to ensure you can keep playing. As long as you don’t go out, good things will definitely happen.
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。



