Special thanks to Alex Hoover, Keewoo Lee and Ali for feedbackand review

One underrated form of privacy, that is not well satisfied by ZK-SNARKs,traditional versions of FHEor other commonly talked about methods, is privatereads. Users want to learn things from a large database,without revealing what they're reading. Some use cases of thisinclude:

• Privacy-preserving Wikipedia (so you can learn things without eventhe server knowing what you're reading)
• Privacy-preserving RAGor LLM search (so yourlocal LLM can get data from the internet without revealing what you'requerying)
• Blockchain data reads (so you can use a dapp that queries anexternal RPC node without the node learning what you're querying; see"private reads" here)

There is a category of privacy protocols that are directly designedto solve this problem, called privateinformation retrieval (PIR). A server has a database \(D\). A client has an index \(i\). The client sends the server a query,the server replies back with an answer that allows the client toreconstruct \(D[i]\), all without theserver learning anything about \(i\).In this post I will describe some basics that underlies all PIRprotocols, and then describe Plinko, a protocol thatefficiently achieves this.

Basics of PIR

To understand more complicated PIR protocols, it's best to start with"classic two-server PIR". Classic two-server PIR assumes that a clientis making queries to two servers, and it truststhat at least one of the two is honest. Here's how the protocolworks:

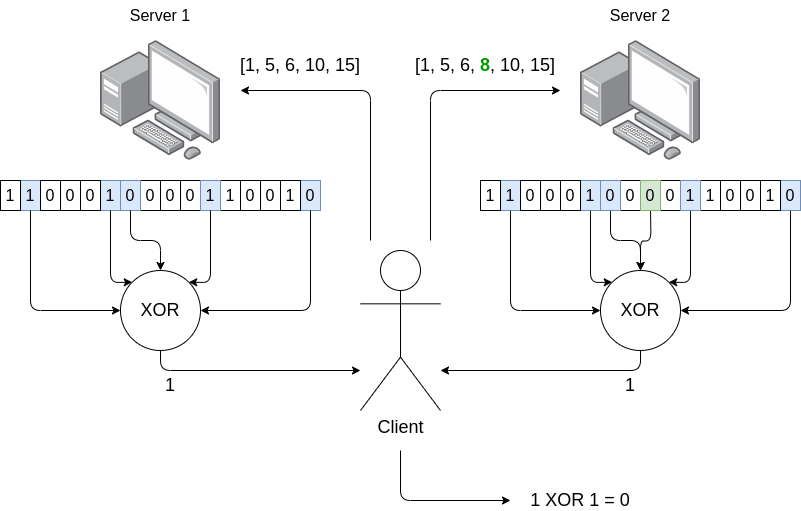
• The client wants to know \(D[i]\),in the above example \(D[8]\).
• The client generates a random subset of indices in \(D\), on average about half full (in theabove example, \([1, 5, 6, 10,15]\)).
• The client sends that subset to one server, and then sends amodified subset, where the membership of \(D[i]\) is flipped (ie. added if it was notthere, removed if it was there), to the other server.
• Each server computes the XOR of the values in \(D[i]\) that it was asked, and returns theresult
• The client XORs these two values, and it gets the value of \(D[i]\)

The key idea is that each server receives what looks like acompletely random subset of the indices. There is not even a slight biasfrom mixing in \(i\), because thatmodification is as likely to add the value as it is to remove it. Thetwo servers give XOR-sums of subsets that are almost identical, butdiffer in one place: one includes \(D[i]\) and the other doesn't. The clientgets these two values, and takes the difference between the two, whichgives \(D[i]\).

This naturally generalizes to "cells" that are bigger than one bit;you could have each \(D[i]\) have eg.1000 bits, and the protocol is exactly the same.

This protocol has three big weaknesses:

1. You have to trust that one of the two servers is honest.
2. The client has communication overhead equal to the number of cells(this can be much smaller than the total size of the data if the cellsare big, but it's still a lot).
3. The server has to XOR half the total data to respond to a singlequery.

There are two well-understood modifications to classic two-server PIRthat solve (1).

One strategy is PIR with preprocessing. Notice thatin the protocol above, you can compute one of the two random sample setsbefore you even know which \(i\) youwant to query for. You generate thousands of these random queries. Youhave an initial phase where you download (but do not need to store) thewhole file \(D\), and you compute theXOR sums for these random sets of indices locally. Essentially, you areacting as one of the two servers - and in this way, satisfy the 1-of-2trust assumption all by yourself, so you do not need to trust the otherserver. This approach does require a huge amount of upfront bandwidth,but you can do it ahead of time, or do it in the background and use amore inefficient form of PIR to answer any queries that you get beforeit finishes.

The other strategy is single-server PIR.Basically, you use some variant of homomorphic encryption (often simplerthan full-on FHE) to encrypt your query, in such a way that the servercan compute on your encrypted query to give you an encrypted answer.This has high computational overhead on the server side, and so is notyet feasible for very large datasets. This strategy can be combined withPIR with preprocessing, so you can theoretically avoid the initialdownload by doing that procedure homomorphically encrypted on the serverside.

Plinko solves (2) and (3) - or at least, it decreases bothcommunication overhead and server-side compute overhead from \(O(N)\) to \(O(\sqrt{N})\) where \(N\) is the number of cells. It uses thepreprocessing strategy to remove the trust assumption. Theoretically,you can do the preprocessing in FHE; it is currently an open problem todo this efficiently enough.

In Plinko's language, there is:

• A setup phase, where the client processes all thedata once (but only remembers a small number of"hints")
• A query mechanism, where the client makes a queryto the server and combines the answer with the right hint to compute theneeded value.

There is also an easy way for the client to update hints if the dataset changes. Now, let's get into the protocol!

Setup phase

Treat the database as being a square, with \(\sqrt{N}\) rows and \(\sqrt{N}\) columns:

The client generates a random master seed \(S\). For each row \(i\), the client uses the master seed togenerate a row seed \(S_i\). The clientgenerates roughly \(128 * \sqrt{N}\)hints. Each hint is generated as follows:

• Randomly (or rather, pseudorandomly by hashing the master seed) pick\(\frac{\sqrt{N}}{2} + 1\) rows
• If we're computing the \(j\)'thhint, for each row \(r_i\), use a hash\(H(S_{r_i}, j)\) to generate a randomcolumn \(c_i\). So we get \(\frac{\sqrt{N}}{2} + 1\) \((r_i, c_i)\) pairs
• XOR the pairs, and save the bit

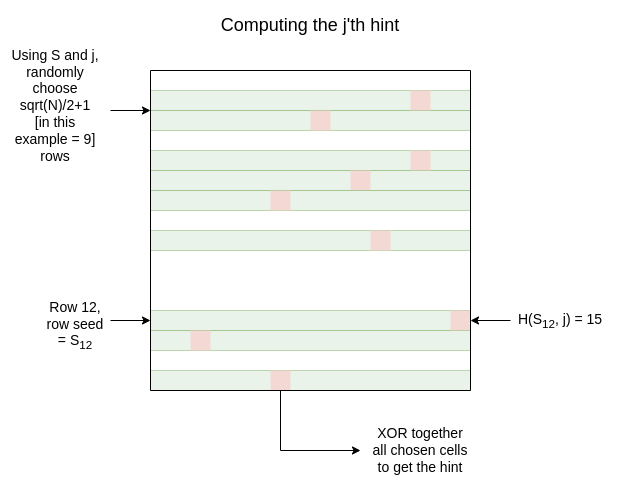
The "hash" that is used to compute the \(c_i\) values could be a regularhash, but that leads to (tolerable but significant) inefficiency duringthe query phase. So instead, Plinko prefers special type of hash calledan "invertible PRF". The core property that it achieves is that given\(S_i\) and \(c_i\), you can easily recover all \(j\) values that lead to that \(c_i\). In practical terms, this means thatfor any cell \((r_i, c_i)\), you caneasily find all hints that "include" that cell.

Additionally, the setup phase generates some "backup hints". Theseare constructed like regular hints, except for each index \(j\), you choose \(\frac{\sqrt{N}}{2}\) rows, and compute apair of hints: one over the chosen subset of rows, and the other for itscomplement (ie. the \(\frac{\sqrt{N}}{2}\) rows that werenot chosen):

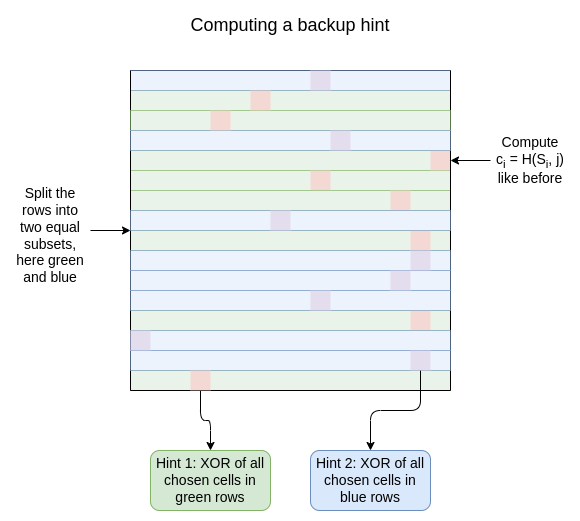
This whole process can be done "streaming", without requiring theclient to store any data at any point in time other than the hintsthemselves. In total, the client needs to download the whole data setand store data equal to roughly \(64 \*\sqrt{N}\) cells, plus \(\sqrt{N}\) cells per backup hint (theclient will need one backup hint for each query that the client willmake).

If desired, the process can also be done in FHE, which means theclient would only need to download the hints, but the server would needto do FHE work over the whole dataset; this is of course expensive, andoptimizing it is an ongoing problem.

Query phase

Suppose you are interested in a specific coordinate \((x, y)\). First, you discover a hint index\(j\) that generates a hint thatcontains \((x, y)\). This is where the"invertible PRF" mechanism helps: it lets you immediately run thefunction in reverse knowing \(S_x\) and\(y\) to compute all \(j\)'s such that \(H(S_x, j) = y\). However, if you want toavoid this complexity, you could just set \(H(S_x, j) = sha256(S_x, \lfloor \frac{j}{16}\rfloor)[j \% 16: (j \% 16) + 2]\) and then compute on average\(\frac{\sqrt{N}}{16}\) hashes everytime.

Then, you determine the \(\frac{\sqrt{N}}{2} + 1\) rows that the hintgenerates. You take out row \(x\). You then send the server a messagethat contains:

• \([(r_1, c_1), (r_2, c_2) ...(r_{\frac{\sqrt{N}}{2}}, c_{\frac{\sqrt{N}}{2}})]\): the set ofpoints included in that hint, except for the point you want
• \([(x_1, y_1), (x_2, y_2) ...(x_{\frac{\sqrt{N}}{2}}, y_{\frac{\sqrt{N}}{2}})]\): the set ofall other rows (including the row you want), with a randomlychosen column for each one

You send these in a random order, so the server does not know whichis which. As far as the server can tell, you just sent it a random setof points, one per row, with the rows split in half in an arbitrary way.The server XORs both sets of cells, and replies with both outputs.

The client then locally takes its hint, XORs it with the (non-junk)value returned by the server, and it has its answer.

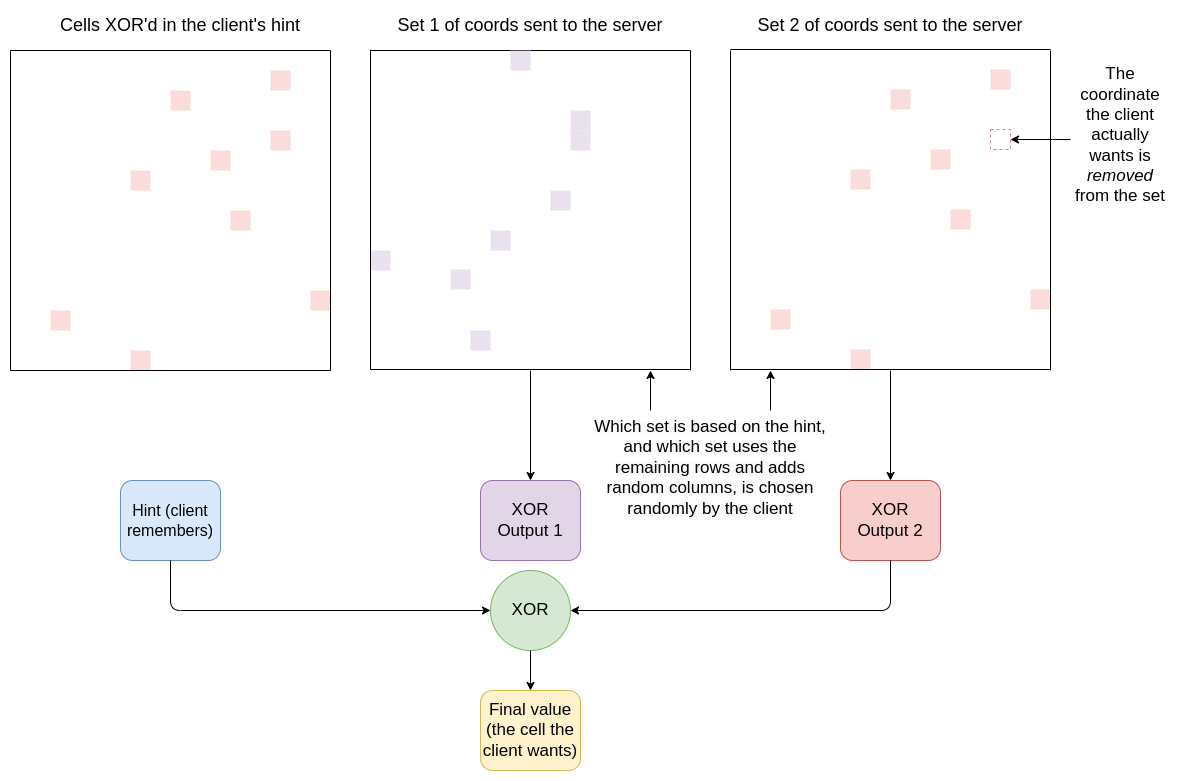
The server does a computation based on \(\sqrt{N}\) cells, and returns that data tothe client. The server knows nothing about which cell the client wants(provided the client does not reuse hints), because the client gave theserver every point in the set in its hint except the point itactually wants. And without knowing the hash that generated thesesubsets, to the server, all the row and column choices look completelyrandom.

Backup queries

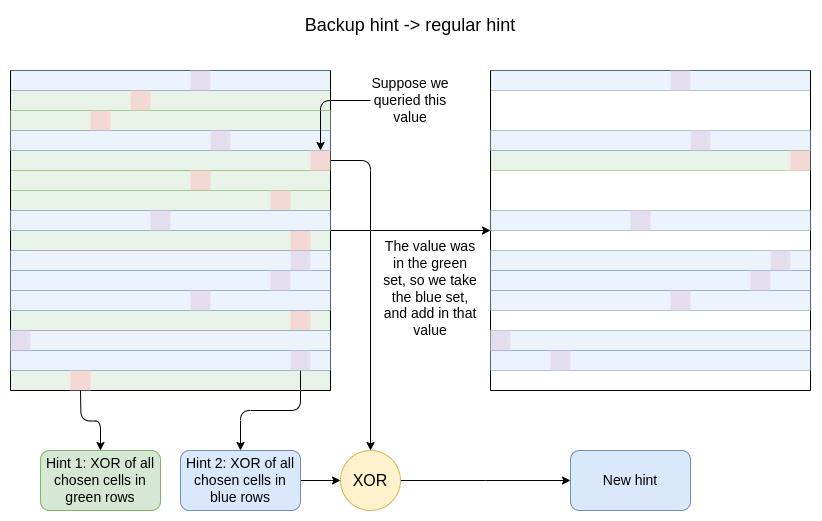
To avoid using a hint twice (and thus leaking data), when the clientmakes a query, it dumps the hint that it used, and "promotes" a backuphint into being a regular hint. Remember that each "backup hint" is apair of hints, one that is based on a random subset of the rows, and theother based on its complement. The algorithm is simple:

• Take the hint value generated from the subset of the rows thatdoes not contain the row you queried
• XOR in the value you queried

Now, you have a set of \(\frac{\sqrt{N}}{2}+ 1\) rows with an XOR of one randomly-chosen column from eachrow: exactly the same format as a regular hint.

Updating the dataset

Suppose a value in the data updates. Then, you can find all hintsthat contain that value, and simply do a direct update: mix in the XORof the old value and the new value.

And that's the whole protocol!

Concrete efficiency

In asymptotic terms, everything in Plinko is \(O(\sqrt{N})\): the size of the hints thatthe client needs to store, the data transmitted per query(technically that's \(O(\sqrt{N} *log(N))\)), and the server-side compute costs. But it helps toput this all into the context of a real-world workload. So let's use thereal-world workload that I am the most familiar with: Ethereum.

Suppose that you are querying a dataset with 10 billion values, eachof which are 32 bytes. This is a pretty good description of the Ethereumstate tree, in a couple of years when it gets significantly bigger dueto scale. We use cuckoo hashingto convert a key-value store into a "flat" lookup table of the type thatPlinko handles.

To include Merkle branches, one simple way (though not the optimalway) is to treat them separately as queries into smaller databases; ifit's a binarytree, then the first level is full-sized, the second level ishalf-sized, the third level is quarter-sized, etc; because PIR costs areall proportional to sqrt, this means that our total costs will all bemultiplied by \(1 + 1 + \frac{1}{\sqrt{2}} +\frac{1}{2} + \frac{1}{2\sqrt{2}} + ... = 3 + \sqrt{2} \approx4.414\). Ethereum's state tree is (for now) a less-efficienthexary tree, but you can ZK-prove equivalence to a binarytree to get the efficiencies of a binary tree today.

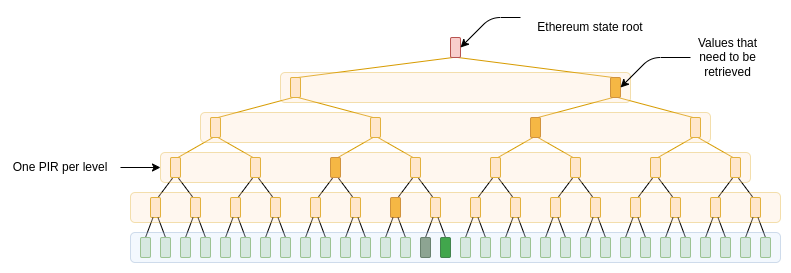
But first, let's provide raw costs without the Merkle branches. Thisimplies a 100000×100000 grid, where each cell is 32 bytes (256 bits).The client would need to store 100000×128 hints, which is 100000 × 128 ×32 bytes ~= 390 MB, plus some extra backup hints.

For each query, the client would need to send the server apartitioning of the rows into two parts, and 100000 column indices. Wecould be super-clever and do slightly better than this, but ifwe do it naively, the row partition is 100000 bits (12.2 kB) and thecolumn indices are 100000 * ceil(log2(100000)) = 1.7m bits = 202.7 kB.These two sum up to 215 kB per query.

If we introduce Merkle branches, the hint costs blow up to about1.68 GB. With clever work, we can actually avoid theper-query communication costs increasing by 4.414x, because we canadjust the PIR in such a way that we use the same (or rather, analogous)query indices for the datasets representing different levels of thetree.

Server-side costs involve reading and XOR'ing 100000 cells, or 3.05MBper query; the XOR is negligible, but the read load is significant.Adding Merkle branches would blow this up to about 13.4 MB in theory,though the realistic added cost may well be negligible because cleverengineering can ensure that matching values are always in the same page(memory pages are usually 4096 bytes).

Our main tool to fiddle with these numbers is to make therectangle unbalanced (have different width and height): we canincrease hint storage by 2x to reduce query size by 2x. Realistically,this is a good tradeoff: storing even 10 GB of hints is not that hard,but especially if nodes are sending multiple queries every 200milliseconds, 215 kB per query is higher than we would be comfortablewith.

In the case of a search engine, the size of the objects would be muchlarger (eg. 10 kB per text webpage), but the number of queries may besmaller. Hence, query complexity would be relatively low, but hint sizewould be large. To compensate for this, it may make sense to make therectangle unbalanced in the other direction.

Beyond Plinko:comparing to the alternatives

One already-existing alternative to Plinko is TreePIR. TreePIR works byusing a "puncturable PRF": a hash function where you can provide a keythat allows evaluating it at all points except for one chosenpoint. This allows you to generate a representation of the query columns("values generated from a seed \(S\)except the \(j\)'th value")that is logarithmic-sized - much more compact than providing the wholelist directly:

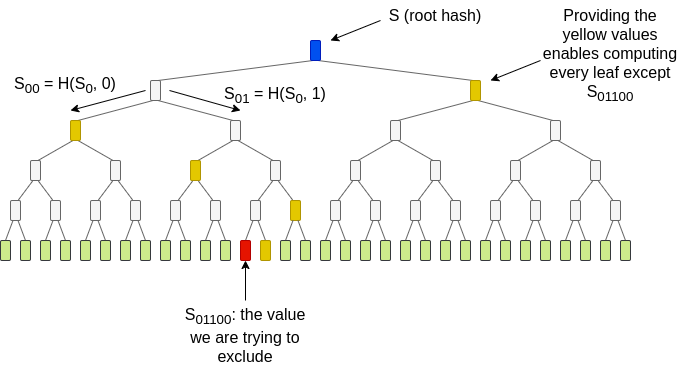
The full approach is somewhat more clever than the above diagram. Theidea in this diagram reveals the excluded index 01100, violatingprivacy. TreePIR works by providing the yellow values withoutrevealing their (horizontal) position in the tree. There are \(2^{log_2(\sqrt{N})} = \sqrt{N}\) possiblesets of leaf values, and thus \(\sqrt{N}\) possible sets of columns, thatcan be generated by taking the left and right choice of position foreach yellow value. The server has an \(O(\sqrt{N} * log(N))\) time algorithm tocompute the XOR sum of chosen cells for every possible arrangementsimultaneously. The client knows which of these sums corresponds to theset that it actually needs. It uses single-server PIR to ask for it.

This reduces communication complexity to logarithmic, at the cost ofincreased server work, and at the cost of removing the "invertible PRF"mechanism, forcing the client to "grind" through many possible hintsuntil they find a matching hint.

There are various theoreticallower boundsfor how much overhead a PIR protocol needs to have. In reality, however,most of these bounds come with caveats, and so the "real" lower boundsare far fewer. For example, if you have obfuscation, you can make any ofthese protocols require only a constant real-time communication overhead- but of course, today, such protocols are still quite far away frompracticality. The harder thing to reduce is server-side computation.Because it's "just" XOR, the workload in Plinko is already not a bigdeal. But if we want to remove the client-side \(O(N)\) download requirement, then we needthe server side to do much heavier computation.

With Plinko, PIR is much further along than it was a decade ago, butthere is still theoretically much further that these protocols couldgo.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。