Compared to the BTC mining machine industry chain, Cellula's solution is a more interesting social experiment.

Authors: Nickaqiao & Faust, Geek Web3

Since the popularity of ERC-20 assets in the blockchain community in 2017, Web3 has entered an era of low-threshold asset issuance. Various project parties have been issuing custom tokens or NFTs at will through methods such as ID0 and IC0, and most of them have strong control or opacity issues. RugPull incidents occur frequently, and various scammers have regarded IC0 and ID0 as excellent ways to exploit users.

Today, conventional ID0 and IC0 have fully exposed their fairness defects. People have always hoped for a more fair and reliable asset issuance protocol to solve many problems when launching new projects. Although some creative projects have unilaterally proposed their "fair economic model," they often fail to be universally promoted, and these economic models mostly end up as "specific cases" rather than "a set of abstract protocols."

So, what kind of model is a more fair and reliable way of distributing assets? What kind of solution can serve as a universal protocol? This article will introduce Cellula, which provides a new perspective to address the above issues. They have implemented a simulated POW asset distribution layer, using virtual proof of work (vPOW) to "mine" the asset distribution process, simulating BTC to achieve a more fair asset distribution paradigm.

Although the project is considered by many as Gamefi, because its distributed in-game rewards can be set as any type of token, Cellula theoretically can serve as an asset distribution platform with POW effects, bringing broader prospects and imaginative space for Web3 asset issuance, and can even be called "a social experiment paying tribute to BTC mining."

POW and vPOW: Unpredictable lottery drawing results

In fact, whether it is authentic POW or POS, or the vPOW we are discussing today, the essence is to set up an algorithm with unpredictable or difficult-to-predict output results, and use the output results for "lottery drawing." BTC miners need to construct a block that meets certain conditions locally and submit it to the full nodes in the network for consensus in order to receive the block reward. As for the conditions, the constructed block's hash must meet special requirements, such as having a prefix of 6 zeros.

Because the generation of block hashes is unpredictable or difficult to predict, constructing a block that meets the conditions can only be achieved by continuously changing the input parameters of the given algorithm. This process requires brute force enumeration and places high demands on the miners' hardware.

In short, BTC mining uses the unpredictability or difficulty to predict of the SHA-256 hash algorithm to implement a "lottery drawing" system with all network miners participating online. This design, at the cost of electricity, ensures a form of permissionless participation.

Furthermore, POW is a more fair way of distributing assets. In mainstream POW public chains, the difficulty for project parties to control the assets is much greater than in POS public chains, while in many POS public chains or IC0 and ID0 schemes, cases of strong control by project parties are common.

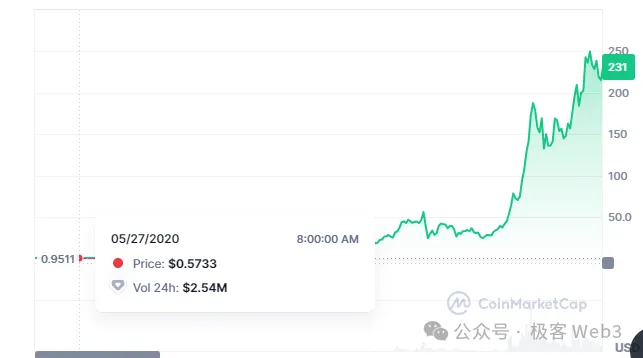
(Under the manipulation of FTX, Solana surged nearly 500 times in 2020-2021, which is extremely unfriendly to latecomer validator operators)

For example, under the manipulation of FTX and SBF, the price of Solana surged nearly 1000 times from 2019 to 2021, and many Solana validator operators were early investors who obtained chips at almost zero cost, severely undermining the fairness of asset distribution. Although project parties also have control over assets in POW, the degree is often much lighter than in POS.

The problem is that the POW model is often applied to the underlying public chain rather than the asset issuance layer of DAPP. Can we simulate the effect of POW with a solution that can be implemented on the chain? If so, a more fair and reliable asset distribution protocol than IC0 and ID0 with strong control can be achieved, and with some gaming scenarios, some interesting Gamefi can be created (of course, the actual use is not limited to games, and it can also provide a fair asset distribution solution for other projects).

So the key question is, if we want to simulate the effect of POW on the asset issuance layer of the chain, how should we do it? In the Cellula Gamefi project introduced in this article, by introducing the famous "Conway's Game of Life" algorithm, they allocate computing power to virtual digital entities on the chain (called "BitLife"). In essence, it's like letting a group of people breed cell clusters in their own petri dishes. As time progresses, the more surviving cells in their petri dishes, the higher the mining power calculated, and the more likely to receive mining rewards.

In short, Cellula replaces the traditional POW hash calculation with another form of unpredictable or difficult-to-predict calculation, replacing the "Work" form in "Proof of Work." In Cellula's approach, the key is how to obtain more surviving cells in the petri dishes (BitLife), and deducing the state changes of BitLife requires consuming computing resources. Essentially, it transforms the hash algorithm executed in BTC mining into a specific algorithm for deducing Conway's Game of Life, which is called vPOW (Virtual POW).

Now let's delve deeper into the mechanism design of vPOW. It must be said that many details here are very interesting. It can be said that one of the things Cellula is doing is simulating the BTC mining machine industry chain model through the chain's NFT trading chain.

vPOW Core: Conway's Game of Life and BitLife

Before we delve into the mechanism design of Cellula, let's first take a look at the most important core of vPOW—Conway's Game of Life. It can be traced back to the concept of "cellular automata" proposed by John von Neumann in 1950, and then mathematician John Conway formally proposed "Conway's Game of Life" in 1970, using an algorithm to simulate the evolutionary laws of life in nature.

Suppose we have a petri dish, and we divide it into a bunch of small squares according to two-dimensional coordinates. Then we perform "initial settings" on the petri dish, allowing some living cells to occupy some squares. After that, the life and death states of these cells will evolve over time, gradually presenting a complex form of cell clusters (you can imagine how mold reproduces). This is essentially a two-dimensional grid game with very simple rules:

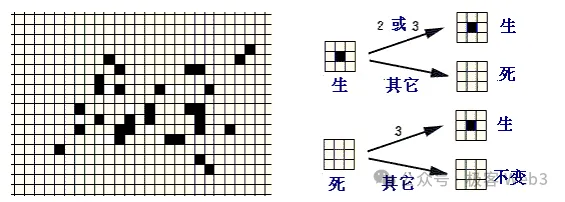
• Each cell has two states: alive or dead, just like the game of Minesweeper, and each cell interacts with the eight cells around it (as shown, black is alive, white is dead);

• If a cell is alive but has fewer than 2 living cells in the 8 cells around it (0 or 1), the cell will die;

• If a cell is alive and has 2 or 3 living cells around it, the cell will remain alive;

• If a cell is alive and has more than 3 living cells around it, the cell will die (simulating a scenario where there are too many living cells competing for resources);

• If a cell is dead but has 3 living cells around it, the cell will become alive (simulating cell proliferation).

So, very simply, given the initial pattern of cell states in a two-dimensional petri dish, and then according to the above rules, the cell states will evolve over time, constantly iterating, and producing a variety of results. You can even use Conway's Game of Life to simulate the effect of a computer.

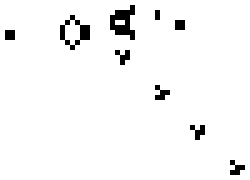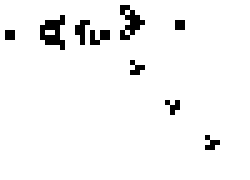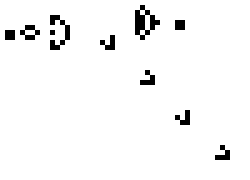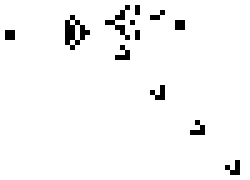
For example, the life/death of each cell in the petri dish corresponds to the binary 0/1. You can consider the initial state of the cells as "input parameters," where the life/death of each cell (0 or 1) represents input data. The cell states will then evolve according to the initial pattern, and each round of state changes is equivalent to a step in the calculation process. After a period of time, the resulting state can be considered as the "output."

As long as an appropriate initial pattern is set, Conway's Game of Life can produce specific results after several generations of evolution. Due to the ever-changing initial patterns, its characteristics can be used to simulate the effect of a lottery drawing. We can set restrictions where each player randomly selects a batch of initial patterns, and after 100 generations of evolution, the petri dish owners whose output results meet certain criteria are eligible for rewards. This is quite similar to the concept of BTC mining:

"The system first defines which output results meet the requirements, and participants input random initial values into the given algorithm, attempting to obtain the desired output results." Due to the large number of initial input parameters to be attempted (almost astronomical), significant effort is required to hit the jackpot, which is the logic behind proof of work: miners must exert a certain amount of effort to receive rewards.

After understanding the basic idea of Cellula and Conway's Game of Life, let's look at the specific design details. Cellula divides the "petri dish" mentioned earlier into 9*9=81 squares, with each cell having two states of life/death (corresponding to binary 0 and 1). As a result, based on permutations and combinations, there are 2^81 initial states for the cells in the petri dish, which is equivalent to the square of 10 trillion (a huge number).

Then, what players need to do is select the initial patterns (input parameters) for the petri dish. BitLife acts as the entity of the petri dish (actually an NFT), containing 81 squares, with each square containing a cell (which can be in a state of life or death, and an empty square is equivalent to a dead cell). Then, each 3*3=9 adjacent squares in BitLife form a BitCell, and each BitLife is composed of 2 to 9 BitCells (if the BitLife constructed by the player does not contain 9 BitCells, some areas will be left empty, defaulting to dead cells).

Based on permutations and combinations, there are 2^9 initial patterns for each BitCell (3*3 squares), and what players need to do is randomly select multiple combinations of different BitCells to construct a BitLife. In simple terms, it means randomly selecting an initial pattern for your petri dish, and as mentioned earlier, there are a total of 2^81 different initial patterns, which is an astronomical number. Therefore, there is a very large space for participants to choose from, which is somewhat similar to the scenario of using SHA-256 in BTC mining.

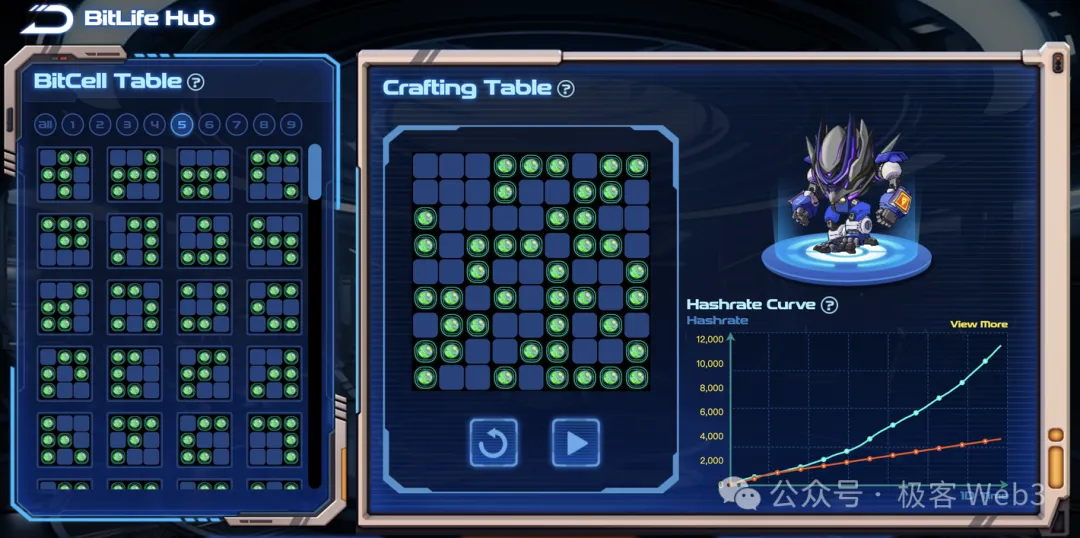
The cell states of BitLife will change as the block height increases. Cellula allocates computing power based on the state of BitLife at different block heights. For a given block height, the more surviving cells a BitLife contains, the higher its computing power. This is equivalent to creating a virtual mining machine.

Here's a specific example: Cellula participants need to exhaustively explore the 2^81 initial patterns of BitLife, predict the states of each pattern after evolution, and see if they meet the requirements of the reward system. For instance, if the current block height is 800 and the system requires that at block height 1000, the BitLife with the most surviving cells will receive the most rewards, then the participants' goal will be clear:

At block height 800, I want to obtain a BitLife pattern that, at block height 1000, will have more surviving cells than other BitLife patterns.

This is actually the core gameplay of Cellula. Your goal is to construct or purchase a BitLife that is most likely to receive mining rewards. This model is akin to allowing ordinary or advanced users to develop their own mining machines, and then you can sell the mining machines you create to others, or purchase others' mining machines for mining. If you want to create your own mining machine, you need to deduce the state evolution of different patterns of BitLife, which will consume computing resources. If you want to buy someone else's mining machine, it means buying BitLife with different initial patterns, and you need to deduce the future state changes of these BitLife patterns, so you still need to calculate on the chain. This is a very interesting aspect of the entire Cellula game design.

After understanding the core mechanism of the game, let's look at other details: In fact, the active cells in BitLife can overflow beyond the initial 99 grid, and the number of surviving cells can be much larger than 99, with no boundary restrictions. As shown in the diagram, if a BitLife contains an increasing number of active cells, its allocated mining power will also increase, and if the initial pattern of the BitLife is chosen poorly, the number of active cells will decrease, and the mining power will also decrease.

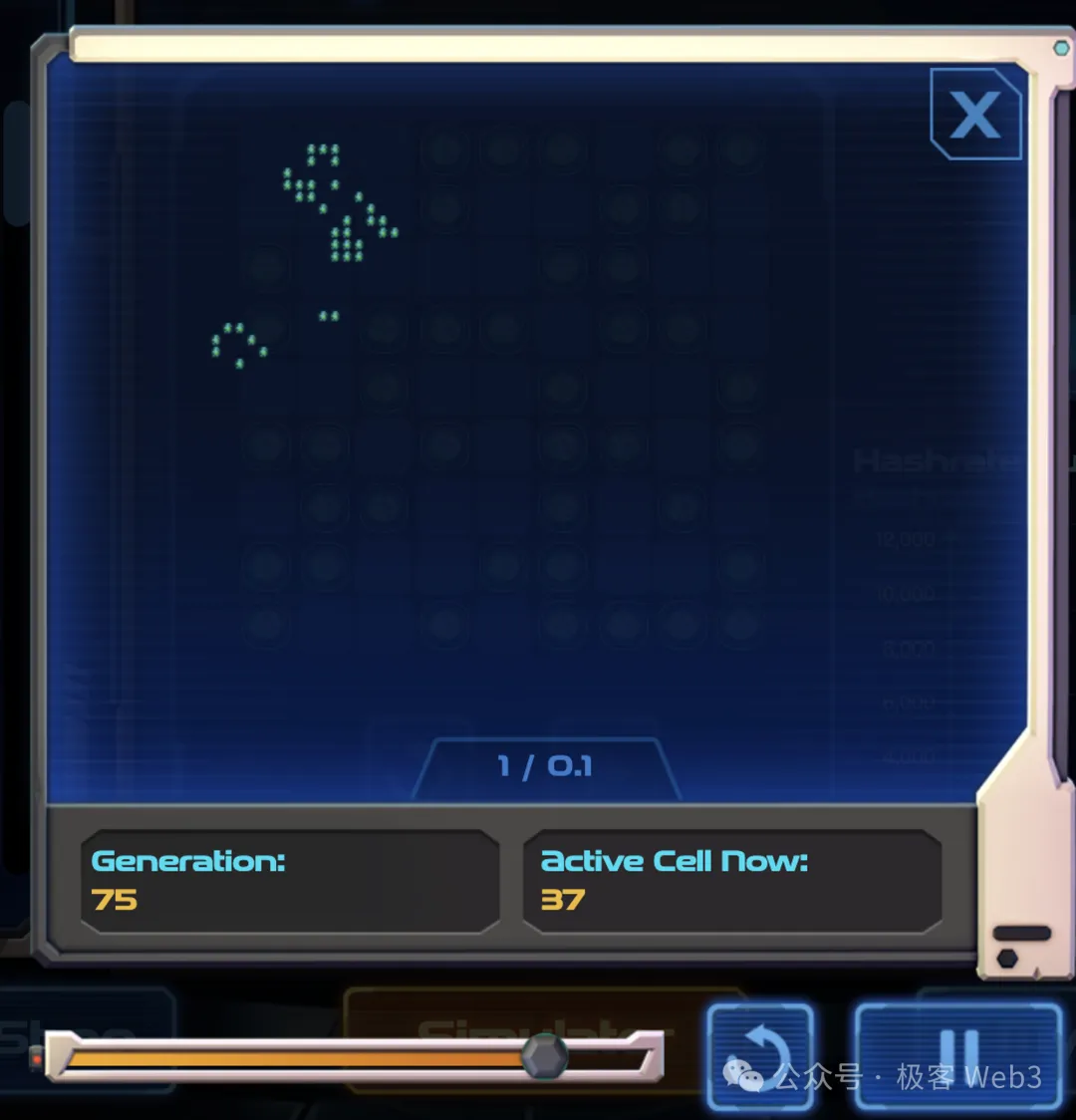
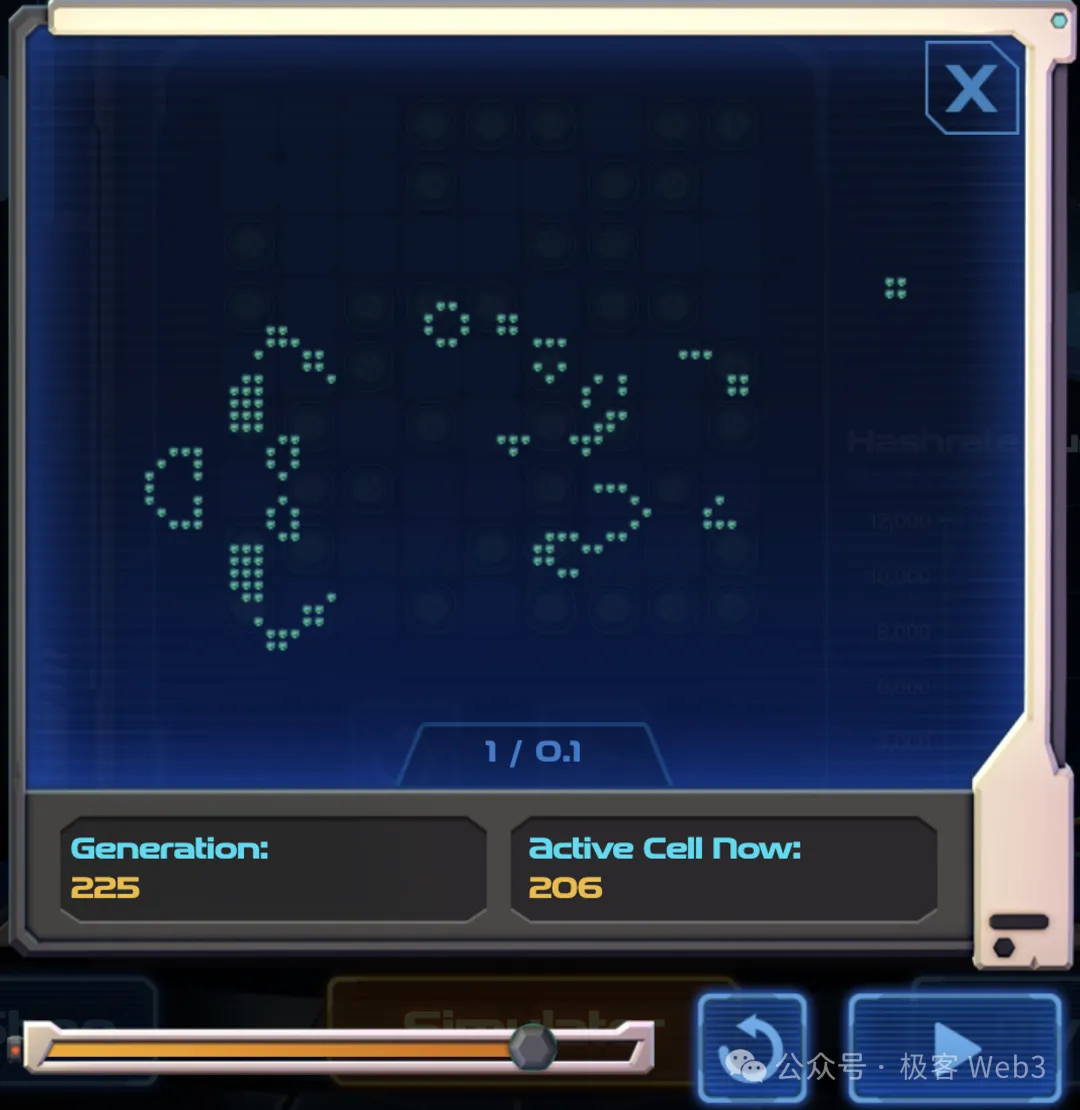
Then, the system will distribute a certain amount of mining rewards (referred to as energy points in the game) every 5 minutes, based on the computing power share of each BitLife in the network.

In Cellula, the process of synthesizing BitLife is akin to the "manufacturing" of new mining machines. As mentioned earlier, BitLife is an NFT, and after being minted on the chain, BitLife needs to be "charged" in order to start mining. The single charge is valid for 1 day, 3 days, or 7 days, and requires a small fee, and recharging is required after it expires.

It's worth mentioning that to encourage users to charge BitLife more, Cellula has implemented a "charging lottery" feature, where each charging operation may result in the user being selected to receive additional rewards (independent of mining rewards). We will briefly introduce this design in the section on the Analysoor algorithm later.

According to Cellula's official rules, the minting of BitLife containing 3*3 BitCells (which includes 81 small squares) has been discontinued, and players have minted over 1.5 million such BitLife. New users can purchase BitLife on the secondary market and engage in charging and mining. According to the official explanation, the limited minting is to maintain the stability of the game ecosystem and prevent scientists from endlessly minting BitLife NFTs, which would devalue the mining machines.

In the future, Cellula will introduce roles similar to mining machine manufacturers, which will be based on permission and require token staking, public sales channels, and a certain community size and influence. These manufacturers will be responsible for minting and selling BitLife containing 4x4 BitCells (which includes 16*9=144 small squares). The quantity of BitLife that manufacturers can mint will be limited by the amount of tokens they stake.

Here's the translation:

Here we have roughly explained the core concepts involved in vPOW in layman's terms. The essence of vPOW is a computational model based on given rules, where participants can compete by optimizing strategies to participate in asset issuance and distribution in a gamified manner. Cellula simulates the operation of the BTC mining machine market, replacing the computational tasks in proof of work. Since the allocation of mining power can be dynamically adjusted, any pattern of BitLife is not necessarily globally optimal. The BitLife with the most surviving cells today may be surpassed by other BitLife tomorrow, leading to complex emergent phenomena and dynamic strategies.

Analysoor Lottery Algorithm and VRGDAs Index Pricing Curve

In the previous section, we mainly elaborated on the core mechanism of Conway's Game of Life and Cellula. Now, let's examine other designs included in the game. As mentioned earlier, Cellula has a charging lottery segment, which uses a random number output algorithm called Analysoor. It uses the block hash as the input parameter for the random number generator to select the winner among the participants in the charging process in each block, introducing a lottery system.

For example, in the design of Analysoor, if the block hash of the current BNB Chain is a long string like 6mjv…, containing the digits 6, 2, 1, 6, the algorithm will use the sorting of these digits in the string to determine the winner. If the first digit is 6, the last digit is 6, and it is even, the algorithm will count from the beginning. The extracted number is counted from 0, so the number 6 corresponds to the 7th transaction, and the 7th charging player in the current block is considered the winner. Of course, the specific design can be more flexible, and this is just an example. This random lottery algorithm effectively incentivizes players to charge more, boosting the activity within the game ecosystem.

Furthermore, in the entire transaction model of Cellula, there is a problem: once a certain pattern of BitLife is minted by a big player, the BitCell combination scheme used will be made public, and others can also "follow suit" and mint BitLife using the same combination scheme, easily leading to a phenomenon of mass imitation, seriously affecting the randomness of the game results. To address this, Cellula has introduced the Variable Rate Gradual Dutch Auction (VRGDAs), a pricing algorithm developed by Paradigm, which dynamically adjusts prices—raising prices when the minting volume exceeds expectations and lowering prices when the minting volume falls short.

For example, if the initial expectation is to mint 10 A-class NFTs per day at a starting price of 1 CKB. By the 5th day, the expected total minting of 50 A-class NFTs is exceeded, reaching 70 due to many people following suit, equivalent to the target originally planned for the 7th day. To control the speed, the exponential pricing curve quickly raises the minting price to 4 CKB per unit to curb minting behavior.

If by the 15th day, only 120 have been minted (the original plan was to mint a total of 150 by this time), falling short of the expected sales volume, the price will be lowered to stimulate minting.

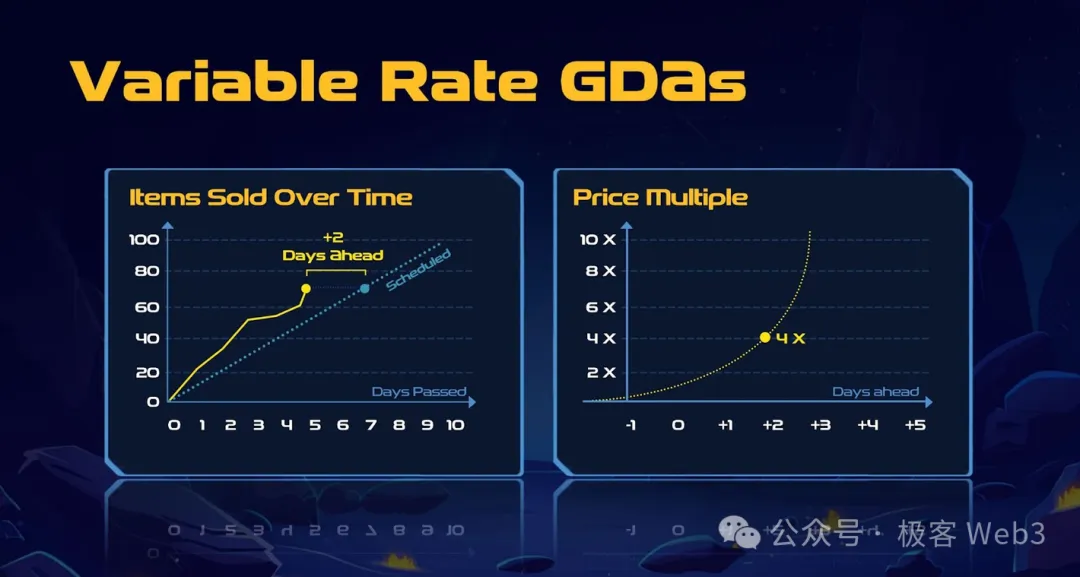
In the above scenario, when a certain type of BitLife is heavily minted in a short period, the minting price of that NFT type will increase exponentially, effectively preventing scientists from monopolizing the market.

Summary: Viewing Cellula from the Players' Game Perspective

After discussing all the core designs of Cellula, let's consider this imaginative game mechanism from the perspective of player interaction. Firstly, in vPOW, there are many participants, each with different strategies. Taking the primary issuance market as an example, a "scientist" can write code and combine different BitCells to find a BitLife with higher computing power, thereby obtaining higher mining rewards. At the same time, there are also MEV players who monitor the minting events on the chain. When they find that a certain scientist has minted a certain type of BitLife, they will also follow suit and mint a large quantity.

However, due to the existence of the VRGDAs exponential pricing algorithm, the minting price of a single type of BitLife can increase exponentially, effectively preventing scientists (or "witches"). This algorithm also prices BitLife/mining machines. If a certain type of mining machine has high computing power, its minting/production price will also be high, and the price in the secondary market will reference the production price, thereby affecting the entire supply chain.

Analogous to the issuance process of BTC mining machines, when a scientist discovers that a certain type of BitLife has high computing power, it is like a mining machine company developing a new chip. MEV players following suit to mint is like a primary distributor setting the price for the mining machine, and the subsequent secondary market transactions are similar to retail investors purchasing equipment from the distributor.

The difference is that compared to the real-world development of mining machines, the speed at which scientists discover new BitLife is much faster, and anyone can participate in deducing the state of BitLife, effectively reducing the power of mining machine development. "Everyone has the opportunity to become a scientist," which is more friendly to the majority of people and is not possible in the real-world mining machine production chain.

For the project itself, adopting a POW-style asset distribution scheme weakens its power. Therefore, whether it's scientists, the project team, or ordinary players, none can unilaterally control the market. In the minting and issuance stages of mining machines, there is a three-way game, and no party can completely monopolize the market, forming a dynamic balance.

Overall, compared to the BTC mining machine industry chain, Cellula's approach is a more interesting social experiment.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。