Title: Fully Homomorphic Encryption: Introduction and Use-Cases

Original Authors: Nicolas Gama and Sandra Guasch, SandBoxAQ

Translation: Faust, GeekWeb3

When it comes to "encryption," the first application scenarios that people usually think of are static encryption and encryption in transit. The former encrypts data and stores it in hardware devices, such as hard drives, mobile devices, or cloud-based servers. In this mode, only authorized individuals can view or modify the decrypted plaintext content. As for encryption in transit, the goal is to ensure that data transmitted over the internet can only be interpreted by specified individuals, even if the data is transmitted through public routers or channels, preventing intermediaries from decrypting the plaintext.

Both of the above scenarios rely on encryption algorithms and also ensure the integrity of the data. This is known as "authenticated encryption": once the data is encrypted, participants in the data transmission process cannot decrypt the plaintext on their own (confidentiality), and no intermediary can arbitrarily tamper with the original ciphertext (integrity/authenticity).

For certain collaborative scenarios, some complex processing of ciphertext is required, which falls under the category of privacy protection technologies, and Fully Homomorphic Encryption (FHE) is one of them. We can take the example of an online voting scenario: suppose in a presidential election, voters can encrypt their voting results and submit them to an intermediary. This intermediary then collects all the voting results, calculates the number of votes for each presidential candidate, and finally announces the final election result.

Unfortunately, when using the aforementioned "authenticated encryption" scheme, the intermediary responsible for tallying the voting results needs to decrypt the plaintext voting data of everyone in order to perform the vote counting task. However, this would expose the voting results of each individual, compromising privacy. In theory, we can shuffle everyone's voting data (some electronic voting protocols do this), but unlike paper ballots, traditional cryptographic mechanisms have difficulty separating the encrypted voting data from the corresponding voter identities while ensuring data integrity (non-tampering).

In an online voting scenario, we can add a hardware isolation barrier around the intermediary responsible for tallying, such as Trusted Execution Environment (TEE). This technology makes it difficult for malicious attackers to interact with the tallying process, but vulnerabilities at the hardware level may lead to the leakage of decryption keys from the TEE. Unlike errors in software, hardware design vulnerabilities are not easily fixed.

To address the above scenarios, we can introduce Fully Homomorphic Encryption (FHE) technology. FHE is a special form of encryption scheme that allows direct computation of ciphertext without decrypting it, obtaining the encrypted result of the function output. This helps protect privacy.

In the context of FHE, the mathematical construction of the function ? is public, so the processing flow of input ciphertext ? and output result ?(?) is public information and can be executed in the cloud without leaking any privacy. It is important to note that both ? and ?(?) are encrypted ciphertext and require decryption keys. In most cases, the decryption keys for both are the same.

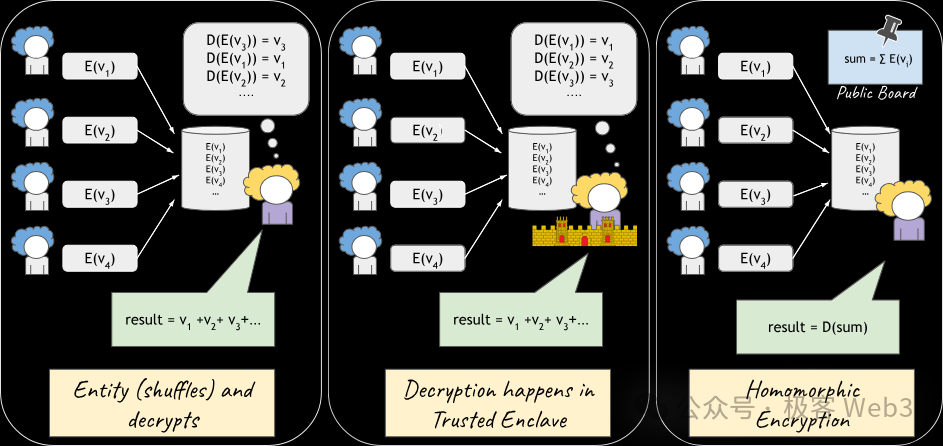
The above image shows three encryption/decryption scenarios for online voting, where E( ) represents the encryption operation and D( ) represents the decryption operation:

In the left image, a trusted intermediary obfuscates and decrypts various voting data before announcing the voting results. We must assume that this intermediary will not disclose privacy and that the voting statistics are accurate.

In the middle image, TEE is used to ensure data integrity and privacy protection.

In the rightmost image, homomorphic encryption technology is used: the encrypted voting data can be publicly aggregated and then decrypted to obtain the results, calculating the final vote count.

FHE (Fully Homomorphic Encryption) is a compact encryption scheme. The size of the ciphertext data for the output result ?(?) and the effort required to decrypt this result depend only on the original plaintext data corresponding to the input data ? and do not depend on the computation process used. This is in stark contrast to non-compact encryption systems, which often simply connect ? and the source code of function ? and let the recipient decrypt ? and input it into ? to complete the computation task.

In reality, the FHE outsourcing mode is often seen as an alternative to secure execution environments such as TEE. The security of FHE is based on cryptographic algorithms and does not depend on physical entities such as hardware. Therefore, FHE is completely unaffected by passive side-channel attacks or attacks on cloud servers. Imagine someone needing to outsource some computing tasks but the data is very sensitive. They may be reluctant to use virtual machines (VMs) built on AWS because there are often higher-level controllers behind such cloud-based servers. They may also hesitate to use things like SGX or TEE because the host running TEE can monitor the power consumption or runtime of the computing task, potentially inferring some information from this data.

However, if FHE is used, the person outsourcing the computing task can be at ease—because in the FHE system, to crack private information, one must crack the cryptographic algorithms used, which is currently almost impossible.

However, while cryptographic algorithms can prevent attackers from decrypting the plaintext corresponding to ?, on the other hand, general expansibility allows attackers to modify the output result ?(?)—this is a form of active side-channel attack. Attackers can target the hardware performing the encryption algorithm, affecting the output result. This may sound frightening, but in the design of FHE, such malicious attacks can be mitigated by introducing redundancy in the computation process.

In summary, FHE typically involves several sets of keys, including the following parts:

Decryption Key: This is the main key in the entire FHE encryption system, and all other types of keys can be derived from the main key. The decryption key is usually generated locally by the user and is never transmitted to the outside world. Only the owner can use it to decrypt FHE ciphertext. This means that even if the ciphertext is intercepted during transmission by others, it cannot be decrypted unless they have the decryption key.

Encryption Key: In the public key mode of FHE, the encryption key is used to convert plaintext into ciphertext. When the person generating the initial ciphertext is not the holder of the decryption key/main key, the encryption key is used for encryption. This key is usually of medium size and consists of some random zero encryption. Since FHE supports affine functions, it is sufficient for encrypting any message.

In public key encryption mode, the encryption key is usually public, and anyone can use it to encrypt data, but only the holder of the decryption key can decrypt it selectively.

Evaluation Key: The evaluation key is a special key used to perform homomorphic operations on the ciphertext ?, allowing the FHE system to perform homomorphic operations on the ciphertext without decrypting it. The evaluation key can be publicly released like a public key. Even if others obtain the evaluation key, they cannot decrypt the ciphertext ? and can only perform homomorphic operations to obtain an output result.

Furthermore, when using the evaluation key for operations, the structure of the ciphertext remains unchanged, and the result obtained from performing homomorphic operations on the ciphertext ? is re-encrypted as a new ciphertext. This ensures the privacy of the computation process, even if the process is public, it will not leak confidential data.

Among the holders of the above types of keys, the holder of the decryption key/main key is the most sensitive. They must ensure that the entire chain/process of homomorphic operations is valid and error-free, and the final ciphertext is secure, and then decrypt to obtain the plaintext result. If malicious operations are introduced into the homomorphic operation chain of FHE, the decryption key may be leaked during decryption. Fortunately, homomorphic operations can be publicly performed and verified by anyone.

Specific Scenarios/Modes of FHE

In this section, we will describe some common scenarios/modes in FHE and discuss the advantages and disadvantages of each mode.

Outsourcing Mode

In this image, the orange key symbol on the left represents the decryption key (and its holder, Alice). FHE ciphertext is represented by locks of the same color as the decryption key. The party contributing private data is represented by a cylinder:

Here, only Alice has contributed private data. On Bob's side, the homomorphic computation function and the evaluation key are publicly available, represented by the green box, and the computation process is deterministic. Everyone can rerun the computation process locally and verify the output results provided by Bob for errors.

The above outsourcing mode is also the first historical application case of FHE, aiming to transform ordinary cloud computing into private computing similar to SGX and TEE. However, the security of the above FHE algorithm is based on cryptographic algorithms, not on hardware-based security measures. In this setup, Alice has some private data but limited computing power, while Bob has a powerful cloud server and does not contribute any additional private data.

Alice can encrypt the input parameters of the computation task ?() to obtain the ciphertext ? and send it to Bob. Bob then computes the result of ?(?) using homomorphic encryption and sends the encrypted result back to Alice.

Given the current performance of hardware devices, the practical promotion of FHE outsourcing mode is relatively slow. If the complexity of the computation task ?() is nonlinear, the time required for FHE computation of ?() will be 1 million times that of the original computation, and the memory overhead will increase by approximately 1000 times. Many organizations are currently developing dedicated FHE hardware to reduce its computational cost, such as the Darpa DPRIVE project or CryptoLight.

Currently, the FHE outsourcing mode is primarily used in the PIR (Private Information Retrieval) scenario, where the controller Bob of the public server has a large public database, and the client Alice initiates a data retrieval request without wanting Bob to know which individuals' data she is interested in. Such PIR scenarios benefit from the linearity and compactness of homomorphic encryption operations, while keeping the computational cost within a reasonable range.

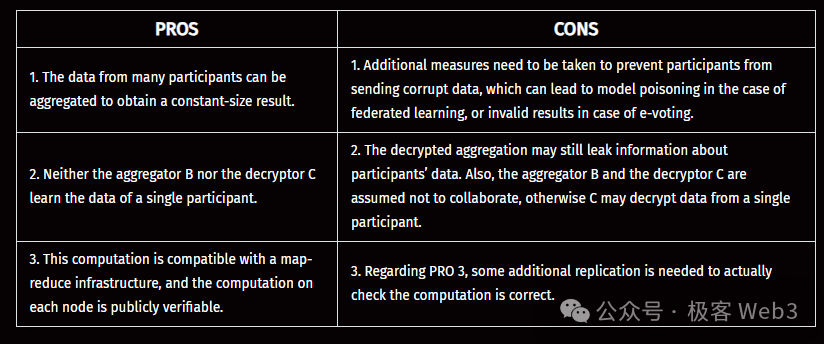
The table below summarizes the advantages and disadvantages of the FHE outsourcing mode.

Two Party Computing Mode

The image uses the same color settings as before. This time, Bob contributes some private data in the computation process. The computation process on Bob's side is no longer publicly verifiable and is represented by a red box. This mode should be limited to scenarios where both parties are honest-but-curious:

In other words, during the protocol execution, participants (such as Bob) strictly follow the given steps for computation and do not intentionally output incorrect results or disrupt the protocol execution. However, Bob is "curious" and will try to infer sensitive information from the ciphertext or other intermediate data encountered, but this will not disrupt the protocol execution.

In the FHE two-party computing mode, the only difference is that Bob contributes some private data to the computation process, integrating his private data into the FHE computation process. In this case, FHE is a good solution for two-party computing, with minimal communication complexity and strong guarantees provided through its mechanism design: Bob will not peek at Alice's private data, and Alice will not peek at Bob's private data.

A potential application case of this scenario is the "millionaire's problem" in cryptography, where Alice and Bob are millionaires who want to know who is wealthier without revealing the exact amount of their assets to each other. The solution to this problem is often used in real-world e-commerce applications.

Aggregation Mode

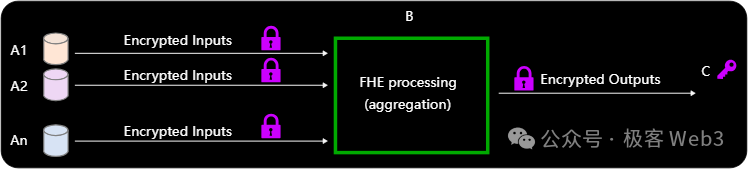
The aggregation mode is an improvement on the outsourcing mode, aggregating data from multiple participants in a compact (output results do not grow with an increase in input parameters) and publicly verifiable manner. Typical use cases include federated learning and online voting systems.

Client-Server Mode

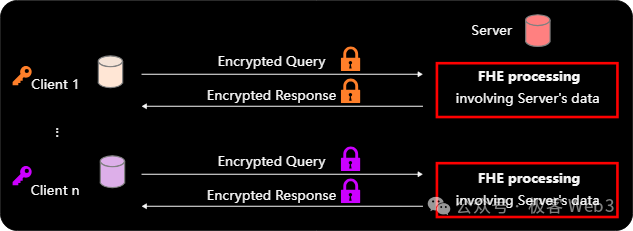
This mode is an improvement on the previously mentioned two-party computing mode, where the server provides FHE computing services for multiple clients with independent keys. FHE can be used for private AI model computation services, for example, where the client has private data and the server has a private AI model or service. The private AI model owned by the server is stored in plaintext locally, and then each client has their own private data and wants to perform computations using the AI model. In the end, each client can use their own key to decipher the computation results of their submitted data.

Other Details about Homomorphic Encryption

How does homomorphic encryption ensure the validity of external computations?

Using FHE in multi-party collaboration scenarios is easier because each participant has the motivation to follow the protocol honestly. For example, FHE can be used to perform encrypted computations and statistics between two legal entities located in different countries but belonging to the same company/organization, such as GDPR regulations allowing the publication of certain statistics externally but prohibiting the centralized storage of all personal data in the same physical location.

In this case, using FHE is feasible, as all participants have the motivation to follow the protocol honestly. In scenarios where participants are not cooperating with each other, the simplest way to ensure that the computation task has been executed correctly is to introduce redundancy (similar to multi-signature/consensus). For example, in the previously mentioned outsourcing and aggregation scenarios, the function formulas used in homomorphic computation are completely public and can be deterministic. As long as two or more independent entities produce exactly the same output ciphertext, the entire computation process is correct, and the result is trustworthy. The higher the level of redundancy, the higher the trustworthiness of the final result, but this requires a trade-off in efficiency.

Furthermore, when the computing party contracted to perform the computation task guarantees the validity of the FHE result by digitally signing the input and output ciphertext, everyone can rerun the same FHE computation process and verify the validity of the proof provided by the computing party. Any deceptive behavior by the computing party can be detected and penalized, and can be associated with a publicly verifiable certificate that will reveal the deception and the deceiver - we call this model the strong covert security model.

As for fully homomorphic signatures, it is another method of verifying the correctness of computations without the need for a third-party verifier, but it typically requires more software and hardware resources to participate.

How does FHE ensure that the final recipient only decrypts the final result and not intermediate variables?

The simplest way is to ensure that the holder of the decryption key cannot access the intermediate ciphertext generated in the FHE computation process. In two-party computing or client-server scenarios, Alice encrypts the input result, Bob computes the ciphertext and transmits the encrypted output result back to Alice. Clearly, Alice can only decrypt the final result and cannot access the intermediate variables.

In cloud-based server scenarios, such as online voting systems, many participants will send encrypted voting data on public cloud servers like AWS. Here, a method is used: the decryption key is usually not given to a single recipient, but is distributed in a secret-sharing manner to different individuals or organizations (similar to MPC). In this case, decryption of specific ciphertext can only be done through multi-party computation and online communication between members holding the decryption key. If some of them refuse to cooperate with others, decryption cannot be performed. This allows the overall security of the system to be enhanced by setting appropriate thresholds.

Building Blocks of Homomorphic Encryption

Homomorphic encryption has three types: partially homomorphic encryption (PHE), leveled homomorphic encryption (LHE), and fully homomorphic encryption (FHE). Partially homomorphic encryption only allows us to perform homomorphic encryption on certain computation tasks (such as summation, linear functions, bilinear functions), while leveled homomorphic encryption and fully homomorphic encryption can support arbitrary computation tasks.

For LHE, the parameters used/generated by the system depend on the function computation ?() to be executed, and increase in complexity of the function computation leads to an increase in the size of ciphertext and keys, consuming more storage and communication resources. On the other hand, FHE schemes allow us to compute any function that can be represented as a binary logic gate circuit under a given set of parameters (i.e., given key and ciphertext sizes). This means that unlike LHE, the parameters (as well as keys and ciphertext) involved in FHE schemes do not increase even as the tasks to be computed become more complex.

Therefore, FHE is the only mode that guarantees that the memory consumption and runtime of homomorphic computation are proportional to the original plaintext/task. However, FHE has a technical issue: as the computation continues, the noise (garbage data) contained in the ciphertext will increase. To avoid excessive noise leading to decryption errors, FHE schemes periodically perform a costly operation called bootstrapping, which can reduce the noise to a controllable level. We will provide more information and education on this in the future, so stay tuned!

Original article link: FHE-01: Understanding the Operating Mode and Application Scenarios of Fully Homomorphic Encryption (FHE)

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。