Decoding the Holy Grail: Challenges and Solutions of On-Chain Fully Homomorphic Encryption

Combining ZKP with Fully Homomorphic Encryption (FHE) can achieve fully universal, encrypted, decentralized finance (DeFi).

Authors: Jeffrey Hu, Arnav Pagidyala

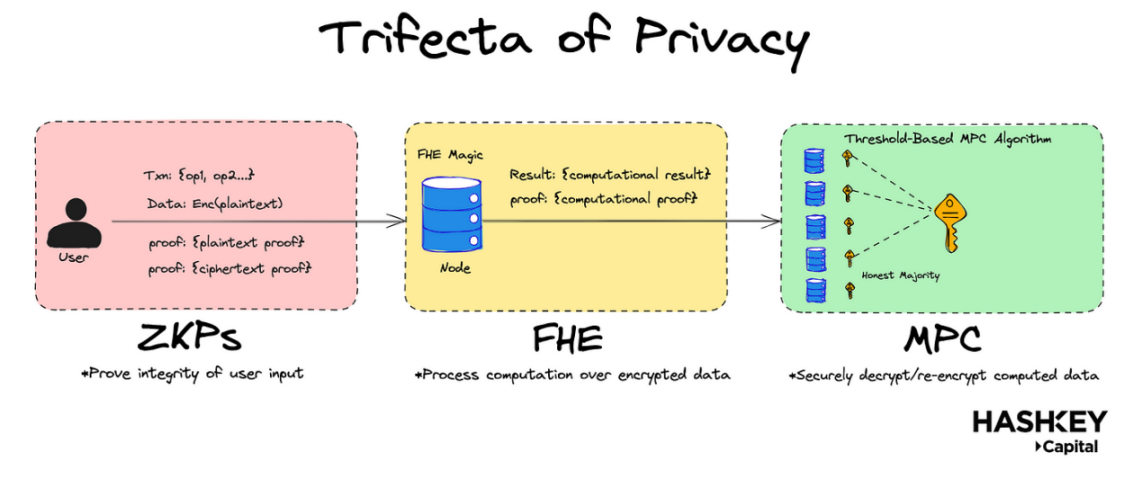
Core Points:

Fully Homomorphic Encryption (FHE) is hailed as the "holy grail of cryptography," but its current applications are limited by performance, development experience, and security.
As shown in the above figure, to build a truly confidential and secure shared state system, FHE needs to be combined with zero-knowledge proofs (ZKPs) and multi-party computation (MPC).
FHE is rapidly developing; the development of new compilers, libraries, hardware, etc., and the research and development of Web2 companies (such as Intel, Google, DARPA, etc.) have greatly promoted the development of FHE.
With the maturity of FHE and its surrounding ecosystem, we expect "verifiable FHE" to become the standard. Decentralized applications (DApps)/rollups may choose to outsource computation and verification to FHE coprocessors.
A fundamental limitation of on-chain FHE is "who holds the decryption key." Threshold decryption and MPC provide solutions to this limitation, but they often involve trade-offs between performance and security.

Introduction:

The transparency of blockchain is a double-edged sword. While its openness and observability are attractive, they are also a concern for enterprises adopting blockchain technology.

On-chain privacy has been one of the most challenging issues in the field of encryption for nearly a decade. Although many teams are building systems based on zero-knowledge proofs (ZKP) to achieve on-chain privacy, they cannot support shared encrypted states. This is because these solutions are a series of ZKP functions, making it impossible to apply arbitrary logic to the current state. This means that we cannot simply use ZKP to build encrypted shared state applications (such as private Uniswap).

However, recent technological breakthroughs indicate that combining ZKP with Fully Homomorphic Encryption (FHE) can achieve fully universal, encrypted, decentralized finance (DeFi). How is this achieved? FHE is an emerging field of cryptography that can perform arbitrary computations on encrypted data. As shown in the figure above, ZKP can prove the integrity of user inputs and computations, while FHE can handle the computations themselves.

Although FHE is hailed as the "holy grail of cryptography," we will attempt to provide an objective analysis of the field and its various challenges and potential solutions. This technical report will cover the following on-chain FHE topics:

FHE Schemes, Libraries and Compilers
Secure Threshold Decryption
ZKPs for User Inputs + Computing Party
Programmable, Scalable DA Layer
FHE Hardware

Fully Homomorphic Encryption (FHE) Schemes, Libraries and Compilers

Challenge: Emerging FHE Schemes, Libraries, and Compilers

The fundamental bottleneck of on-chain FHE lies in the lagging development tools and infrastructure. Unlike zero-knowledge proofs (ZKP) or multi-party computation (MPC), FHE has had a relatively short development time since 2009, resulting in lower maturity.

The main limitations of the FHE development experience include:

Lack of user-friendly front-end languages that allow developers to code without needing an in-depth understanding of backend cryptography.
Lack of fully functional FHE compilers capable of handling all complex tasks (such as parameter selection, BGV/BFV SIMD optimization, and parallel optimization).
Existing FHE schemes (especially TFHE) are approximately 1000 times slower compared to regular computation.

To truly understand the complexity of integrating FHE, let's take a look at the process developers have to go through:

The first step in integrating FHE into an application is to choose an FHE scheme. The table below explains the main schemes:

As shown in the table above, Boolean circuits (such as FHEW and TFHE) have the fastest bootstrapping speed, can avoid complex parameter selection processes, and can be used for arbitrary/generic computation, but are relatively slow; while BGV/BFV is suitable for general DeFi applications because they are more efficient in high-precision arithmetic calculations, but developers must know the depth of the circuit in advance to set all scheme parameters. On the other hand, CKKS supports homomorphic multiplication, allowing for precision errors, making it suitable for non-precise use cases, such as machine learning.

As a developer, you need to carefully choose an FHE scheme, as it will affect all other design decisions and future performance. Additionally, several key parameters are crucial for correctly setting up an FHE scheme, such as the choice of modulus size and the effect of polynomial degree.

Next, let's discuss libraries. The table below shows the functionalities and capabilities of the most widely used FHE libraries:

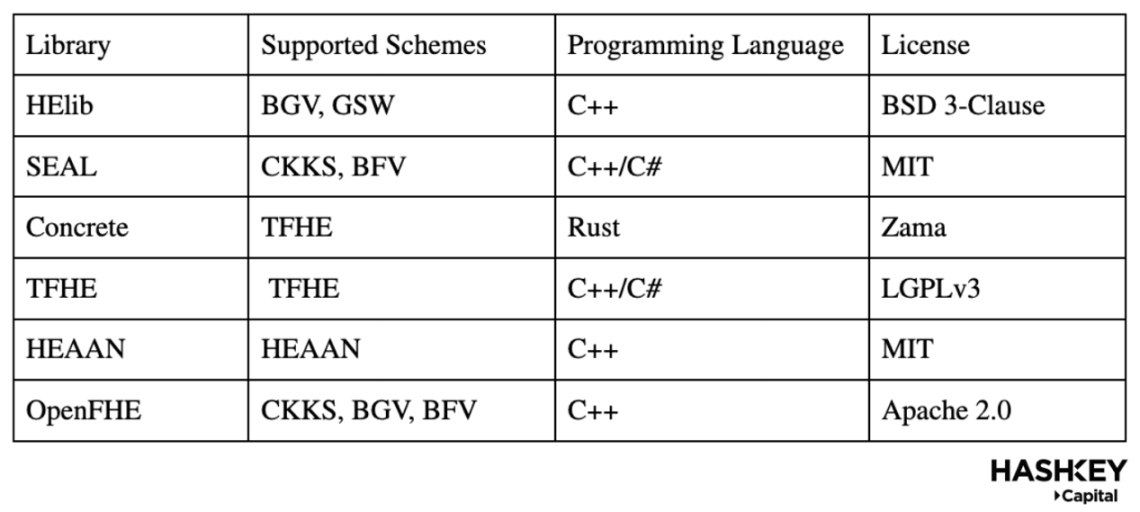
However, these libraries have different relationships with different FHE schemes and compilers, as shown below:

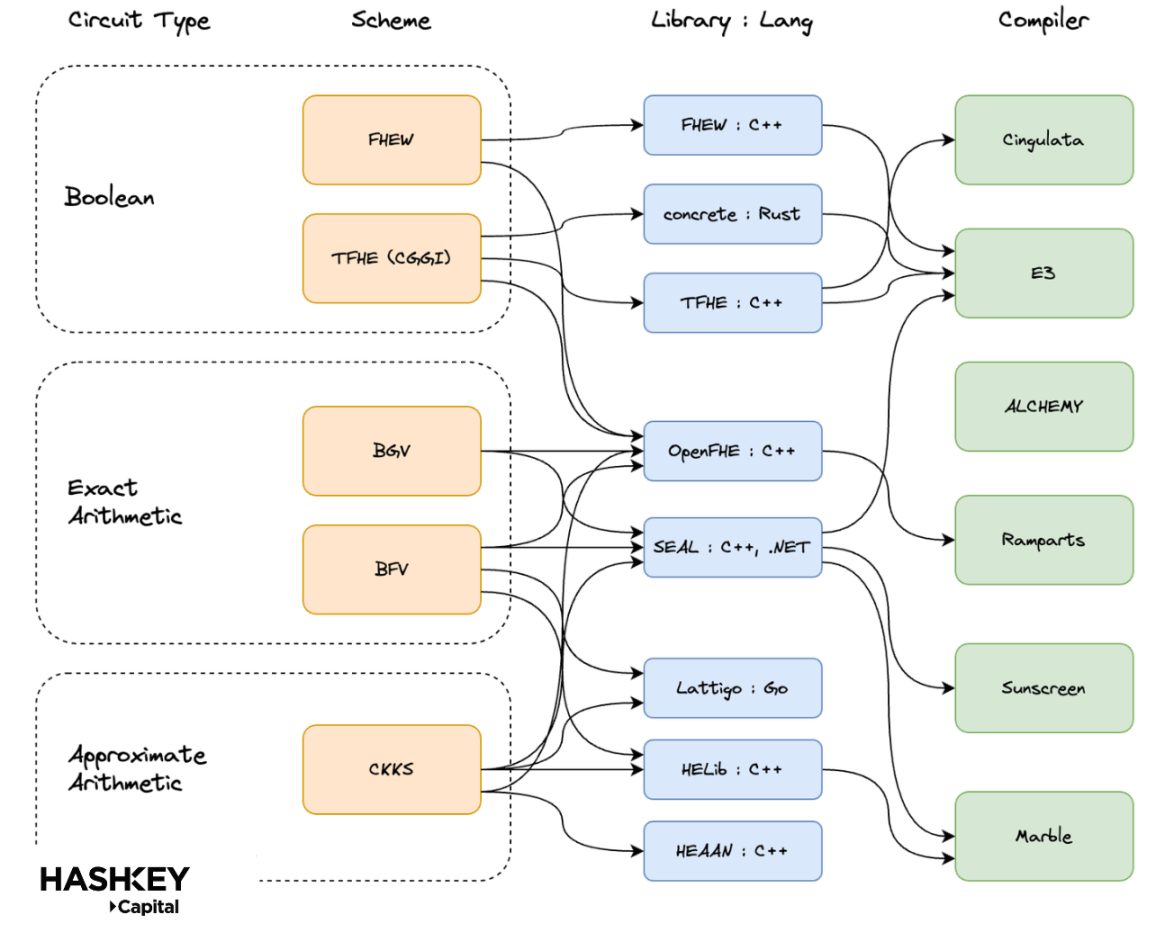
Once an FHE scheme is chosen, developers need to set parameters. Correctly choosing parameters will have a huge impact on the performance of the FHE scheme. Comparatively difficult is the need for an understanding of abstract algebra, FHE-specific operations (such as relinearization and modulus switching), and arithmetic or binary circuits. Finally, to effectively choose parameters, it is necessary to conceptually understand how they affect the FHE scheme.

At this point, developers may ask:

How large does my plaintext space need to be? How large can the ciphertext be? Where can I perform parallel computation? And so on…

Furthermore, although FHE can support arbitrary computation, developers need to change their mindset when writing FHE programs. For example, the program cannot write a branch (if-else) based on variables, as the program cannot directly compare variables as ordinary data. Instead, developers need to change the code from a branch to some kind of computation that includes all branch conditions. Similarly, this also prevents developers from writing loops in the code.

In summary, for developers unfamiliar with FHE, integrating FHE into their applications is almost impossible. This will require significant development tools and infrastructure to abstract the complexity presented by FHE.

Solution:

1. Web3-specific FHE Compiler

Although FHE compilers built by companies such as Google and Microsoft already exist, they:

Not designed for performance, adds a 1000x "overhead" compared to directly writing circuits
Optimized for CKKS (i.e., ML), not as beneficial for BFV/BGV required for DeFi
Not built for Web3. Incompatible with ZKP schemes, programmable blockchains, etc.

Until the emergence of the Sunscreen FHE compiler. It is a Web3-native compiler that provides optimal performance for arithmetic operations (e.g., DeFi) without the need for hardware accelerators. As mentioned above, parameter selection may be the most difficult part of implementing an FHE scheme. Sunscreen not only automates parameter selection but also implements data encoding, key selection, relinearization and modulus switching, circuit setup, and SIMD operations.

With technological advancements, we expect to see further optimizations not only in the Sunscreen compiler but also from other teams building their own, supporting other high-level languages.

2. New FHE Libraries

While researchers continue to explore new effective solutions, FHE libraries can also enable more developers to integrate FHE.

Take FHE smart contracts, for example. Although choosing from different FHE libraries may be challenging, it becomes easier when we talk about on-chain FHE, as there are only a few dominant programming languages in Web3.

For example, Zama's fhEVM integrates Zama's open-source library TFHE-rs into a typical EVM, exposing homomorphic operations as precompiled contracts. Effectively allowing developers to use encrypted data in their contracts without any changes to the compilation tools.

For other specific scenarios, some additional infrastructure may be required. For example, the TFHE library maintained in C++ is not as well-maintained as the Rust version. Although TFHE-rs can support C/C++ exports, if C++ developers want better compatibility and performance, they must write their own version of the TFHE library.

Finally, a core reason for the lack of FHE infrastructure in the market is the lack of an effective way to build FHE-RAM. One possible direction is to research an FHE-EVM without certain opcodes.

Secure Threshold Decryption

Challenge: Insecure/Centralized Threshold Decryption

Every confidential shared state system is based on encryption and decryption keys. Since no single party can be trusted, the decryption key is fragmented among network participants through multi-party computation (MPC).

One of the most challenging aspects of on-chain Fully Homomorphic Encryption (FHE) is building a secure and high-performance threshold decryption protocol. There are two main bottlenecks: (1) FHE-based computations introduce significant "overhead," requiring high-performance nodes, which essentially reduces the potential size of the validator set; (2) as the number of nodes participating in the decryption protocol increases, the latency also increases.

So far, FHE protocols rely on an honesty majority in the validators. However, as mentioned above, on-chain FHE implies a smaller validator set, thus increasing the likelihood of collusion and malicious behavior.

What if threshold nodes collude? They would be able to bypass the protocol, essentially decrypting anything, including user inputs to any on-chain data. Furthermore, it is important to note that the decryption protocol in the current system can occur without being detected (i.e., "silent attacks").

Solution: Improved threshold decryption or dynamic MPC

There are several possible approaches to address the drawbacks of threshold decryption: (1) enabling an n/2 threshold, making collusion more difficult; (2) running the threshold decryption protocol inside hardware security modules (HSM); (3) using a threshold decryption network based on trusted execution environments (TEE), controlled by a decentralized chain, allowing dynamic key management.

Instead of relying on threshold decryption, it is more likely to use MPC. An exemplary instance of an MPC protocol that can be used in on-chain FHE is Odsy's new 2PC-MPC, the first non-colluding and large-scale decentralized MPC algorithm.

Another approach may be to encrypt data using only the user's public key. Then, validators process homomorphic operations, and the user can decrypt the result when necessary. While this is only applicable to specific use cases, it allows us to completely avoid threshold assumptions.

In summary, on-chain FHE requires an efficient MPC implementation with the following characteristics: (1) able to work even in the presence of malicious actors; (2) introduces minimal latency; (3) allows permissionless/flexible node participation.

Zero-Knowledge Proofs (ZKP) for User Inputs and Computing Party

Challenge: Verifiability of User Inputs and Computations

In the Web2 world, when we request the execution of a computational task, we completely trust that a company will run this task behind the scenes as they promised. In Web3, this model is completely reversed. We no longer rely on a company's reputation and simply trust them to act in good faith, but operate in a trustless environment, meaning users should not need to trust anyone.

While Fully Homomorphic Encryption (FHE) allows for processing encrypted data, it cannot verify the correctness of user inputs or computations. Without the ability to verify, FHE is almost useless in the context of blockchain.

Solution: ZKP for User Inputs and Computing Party

While FHE allows anyone to perform arbitrary computations on encrypted data, ZKP allows people to prove something is true without revealing the underlying information itself. So how are they related?

FHE and ZKP are combined in three key ways:

Users need to submit a proof that their input ciphertext is in the correct format. This means the ciphertext complies with the requirements of the encryption scheme, not just any arbitrary data string.
Users need to submit a proof that their input plaintext satisfies the conditions of a given application. For example, the account balance is greater than the transfer amount.
Validators (i.e., computing party) need to prove that they have correctly executed the FHE computation. This is called "verifiable FHE" and can be seen as an analogy to the ZKP required for rollups.

To further explore the application of ZKP:

1. ZKP for Ciphertext

FHE is based on lattice-based cryptography, meaning the construction of encryption primitives involves lattices, which are post-quantum secure. In contrast, popular ZKP such as SNARKs, STARKs, and Bulletproofs do not rely on lattice-based cryptography.

To prove the correctness of a user's FHE ciphertext format, we need to demonstrate that it satisfies a matrix-vector equation with elements from rings and that these elements have small values. Essentially, we need a proof system designed for processing lattice-based relations that is cost-effective for on-chain verification, which is an open area of research.

2. ZKP for Plaintext Inputs

In addition to proving the correctness of ciphertext format, users also need to prove the validity of their input plaintext using general SNARKs, allowing developers to leverage existing ZKP schemes, libraries, and infrastructure.

However, the challenge is that we need to "link" these two proof systems. Linking means ensuring that the user has used the same inputs for both proof systems. Otherwise, malicious users may deceive the protocol. It is important to emphasize that this is an extremely difficult cryptographic endeavor and an open area of early research.

Sunscreen has laid the groundwork for this, as their ZKP compiler supports Bulletproofs, as it is the easiest to connect with SDLP. Research on "linking" FHE and ZKP compilers is also ongoing.

Mind Network has been at the forefront of integrating ZKP to ensure zero-trust inputs and outputs while leveraging FHE for secure computation.

3. ZKP for Correct Computation

Running FHE on existing hardware is extremely inefficient and expensive. As seen in the dynamic manifestation of the scalability trilemma, networks with high node resource requirements cannot scale to a decentralized level. A possible solution is a process called "verifiable FHE," where the computing party (validator) submits a ZKP to prove the honest execution of transactions.

An early prototype of verifiable FHE can be demonstrated through a project called SherLOCKED. Essentially, FHE computations are loaded onto the Bonsai zkVM of Risc ZERO, which processes encrypted data computations off-chain and returns results with ZKP, updating the state on-chain.

An example of recent use of an FHE coprocessor is Aztec's on-chain auction demo. Unlike existing FHE chains that use threshold key encryption for the entire state, meaning the system's strength depends solely on its threshold committee, in Aztec, users own their data and are not bound by threshold security assumptions.

Finally, it is important to understand where developers can first build FHE applications. Developers can build their applications on FHE-supported L1, FHE rollups, or on any EVM chain and utilize an FHE coprocessor. Each design has its own trade-offs, but we lean towards well-designed FHE rollups (pioneered by Fhenix) or FHE coprocessors, as they inherit security benefits from Ethereum.

Until recently, implementing fraud proofs on FHE-encrypted data has been complex, but the team at Fhenix.io recently demonstrated how to use the Arbitrum Nitro stack to compile FHE logic into WebAssembly to achieve fraud proofs.

FHE Data Availability (DA) Layer

Challenge: Lack of Customizability and Throughput

While "storage" has been commoditized in Web2, the same cannot be said for Web3. Considering the over 10,000x data inflation maintained by Fully Homomorphic Encryption (FHE), we need to determine where to store large amounts of FHE ciphertext. If every node operator in a given DA layer needs to download and store data from every FHE chain, only institutional operators can keep up with the demand, increasing centralization risks.

In terms of throughput, Celestia's maximum speed is 6.7 MB/s. If we want to run any form of FHEML, we would need gigabytes of bandwidth per second. According to recent data shared by 1k(x), existing DA layers cannot support FHE due to design decisions limiting throughput intentionally.

Solution: Horizontal Scalability + Customizability

We need a DA layer that can support horizontal scalability. Existing DA architectures propagate all data to every node in the network, which is a major limitation to scalability. Instead, with more DA nodes entering the system, horizontal scalability means each node stores less data, improving performance and cost as more block space becomes available.

Additionally, given the large size of data associated with FHE, providing developers with a higher level of erasure coding thresholds customization makes sense. In other words, to what extent are developers comfortable with the guarantees of the DA system? Is it based on equity-weighted or decentralized-weighted?

The architecture of EigenDA could serve as a foundation for a possible FHE DA layer. Its horizontal scalability, reduced structural cost, decoupling of DA and consensus, pave the way for scalable support of FHE.

Finally, a higher-dimensional idea may be to build optimized storage slots for storing FHE ciphertext, as the ciphertext follows specific encoding schemes, optimized storage slots may help efficiently utilize storage space and retrieve data faster.

Fully Homomorphic Encryption (FHE) Hardware

Challenge: Low-Performance Fully Homomorphic Encryption (FHE) Hardware

In the promotion of on-chain Fully Homomorphic Encryption (FHE) applications, a major issue is the significant latency caused by computational overhead, making running FHE on standard processing hardware impractical. This limitation stems from the extensive interaction with memory, as the processor needs to handle a huge amount of data. In addition to memory interaction, complex polynomial calculations and time-consuming ciphertext maintenance operations also incur significant overhead.

To understand the state of FHE accelerators, we need to uncover the specific design aspects: application-specific FHE accelerators versus generalized FHE accelerators.

The core of FHE's computational complexity and hardware design always relates to the number of multiplications required for a given application, known as the "depth of homomorphic operations." In specific application cases, the depth is known, and thus system parameters and related computations are fixed. Therefore, hardware design for specific applications will be easier and can often be optimized for better performance than generalized accelerator designs. In general, if FHE needs to support an arbitrary number of multiplications, bootstrapping technology needs to be introduced to remove accumulated noise in homomorphic operations. Bootstrapping technology is costly and requires a large amount of hardware resources, including chip memory, memory bandwidth, and computation, meaning hardware design will be very different from that of generalized accelerators. Therefore, while industry players such as Intel, Duality, SRI, DARPA, etc., are undoubtedly working to push the limits in GPU and ASIC design, they may not be directly applicable to support blockchain scenarios.

In terms of development costs, generalized hardware requires more capital for design and manufacturing than application-specific hardware, but its flexibility allows the hardware to be used in a wider range of applications. On the other hand, for specific application designs, if the application's requirements change and need to support deeper levels of homomorphic computation, the specific application's hardware needs to be combined with some software techniques (such as MPC) to achieve the same purpose as generalized hardware.

It is worth noting that supporting on-chain FHE is much more difficult compared to specific use cases (such as FHEML), as it requires the ability to handle more general computations rather than a more specific set. For example, the current transaction processing speed of the fhEVM development network is limited to single-digit TPS.

Considering the need for custom FHE accelerators for blockchain, another consideration is: how transferable is the ZKP hardware to FHE hardware?

There are some common modules between ZKP and FHE, such as Number Theoretic Transform (NTT) and underlying polynomial operations. However, the bit width of NTT used in these two cases is different. In ZKP, the hardware needs to support multiple bit widths of NTT, such as 64-bit and 256-bit, while in FHE, due to the use of residue number systems, the operands of NTT are shorter. Additionally, the NTT degree processed in ZKP is usually higher than in FHE. Due to these reasons, designing an NTT module that satisfies developers for both ZKP and FHE is not an easy task. In addition to NTT, there are other computational bottlenecks in FHE, such as automorphism, which do not exist in ZKPs. One way to simply transfer ZKP hardware to an FHE setting is to load the NTT computation task onto ZKP hardware and use CPU or other hardware to handle the remaining computations in FHE.

In summary of these challenges, performing computations on encrypted data with FHE used to be 100,000 times slower than on plaintext data. However, due to newer encryption schemes and recent developments in FHE hardware, the current performance has significantly improved to be only about 100 times slower than plaintext data.

Solutions:

1. Improvements in FHE Hardware

Many teams are actively building FHE accelerators, but they have not focused on FHE accelerators specific to generalized blockchain computations (e.g., TFHE). An example of a specific hardware accelerator for blockchain is FPT, a fixed-point FPGA accelerator. FPT is the first hardware accelerator that heavily utilizes inherent noise in FHE computations, fully implementing TFHE bootstrapping using approximate fixed-point arithmetic. Another project that may be useful for FHE is BASALISC, a series of hardware accelerator architectures designed to significantly accelerate FHE computations in the cloud.

As mentioned earlier, a major bottleneck in FHE hardware design is the extensive interaction with memory. To bypass this obstacle, a potential solution is to minimize interaction with memory as much as possible. Processor-in-memory (PIM) or near-memory computation may be helpful in this case. PIM is a promising solution to address the "memory wall" challenge in future computer systems, allowing memory to simultaneously perform computing and storage functions, promising a fundamental reform of the relationship between computing and memory. Significant progress has been made in non-volatile memory design over the past decade, such as resistive RAM, spin-transfer torque magnetic RAM, and phase-change memory. Using such special memory, research has shown significant improvements in computational performance in machine learning and lattice-based public key encryption.

2. Optimized Software and Hardware

In recent developments, software has been recognized as a key component in hardware acceleration processes. For example, renowned FHE accelerators such as F1 and CraterLake use compilers for mixed software-hardware co-design.

With the advancement in this field, we can expect fully-featured compilers co-designed with FHE compilers tailored for blockchain. FHE compilers can optimize FHE programs based on the cost model of the corresponding FHE scheme. These FHE compilers can integrate with FHE accelerator compilers to improve end-to-end performance by combining hardware-level cost models.

3. Networked FHE Accelerators: From Vertical to Horizontal Scaling

Existing efforts in FHE hardware acceleration have mainly focused on "vertical scaling," which involves focusing on vertical improvements of individual accelerators. On the other hand, "horizontal scaling" focuses on connecting multiple FHE accelerators through a network, which could significantly improve performance, similar to parallel proof generation with zero-knowledge proofs (ZKPs).

A major difficulty in FHE acceleration is the data expansion issue: the significant increase in data size during encryption and computation, posing challenges for efficient data transfer between on-chip and off-chip memory.

Data expansion poses a significant challenge for horizontally connecting multiple FHE accelerators through a network. Therefore, the joint design of FHE hardware and network will be a promising direction for future research. For example, adaptive network routing for FHE accelerators: implementing a mechanism to dynamically adjust data paths between FHE accelerators based on real-time computational loads and network traffic. This will ensure optimal data transfer rates and efficient resource utilization.

Conclusion

FHE will fundamentally reshape the way we protect data across various platforms, paving the way for an unprecedented new era of privacy. Building such a system will require significant progress in FHE, zero-knowledge proofs (ZKPs), and multi-party computation (MPC).

As we enter this new field, collaborative efforts between cryptographers, software engineers, and hardware experts will be essential. Not to mention legislators, regulators, etc., as compliance is the only way to achieve mainstream adoption.

Ultimately, FHE will stand at the forefront of the digital sovereignty revolution, heralding a future where data privacy and security are inseparable.

Special Thanks

A big thank you to Mason Song (Mind Network), Guy Itzhaki (Fhenix), Leo Fan (Cysic), Kurt Pan, Xiang Xie (PADO), Nitanshu Lokhande (BananaHQ) for their review. We encourage readers to learn about the impressive work and efforts of these individuals in this field!

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。