Is Transformer destined to be unable to solve new problems beyond "training data"?

Original source: Synced

Image source: Generated by Wujie AI

When it comes to the impressive capabilities demonstrated by large language models, one of them is the ability to learn from few samples by providing context in the form of samples and asking the model to generate a response based on the final input. This relies on the underlying machine learning technology "Transformer model," and they can also perform context learning tasks outside of language.

Past experience has shown that for task families or function classes well represented in the pre-trained mixture, the cost of choosing an appropriate function class for context learning is almost zero. Therefore, some researchers believe that Transformers can generalize well to tasks/functions with the same distribution as the training data. However, a lingering question is: how do these models perform on samples that are not consistent with the training data distribution?

In a recent study, researchers from DeepMind explored this question through empirical research. They framed the generalization problem as follows: "Can a model generate good predictions with in-context examples from a function not in any of the base function classes seen in the pretraining data mixture?"

This paper focuses on a specific aspect of the pre-training process: "the data used in pre-training," and investigates how it affects the few-shot learning capabilities of Transformer models produced as a result. To address this question, the researchers first explored the model selection ability between different function class families seen during pre-training (Section 3), and then addressed several key out-of-distribution (OOD) generalization problems (Section 4).

Link to the paper: https://arxiv.org/pdf/2311.00871.pdf

They found: first, pre-trained Transformers struggle to predict convex combinations of functions extracted from the pre-trained function classes; second, while Transformers can effectively generalize over rarer parts of the function class space, they still collapse when tasks become out-of-distribution.

In summary, the inability of Transformers to generalize beyond the pre-training data leads to the inability to solve problems beyond what they have been trained on.

Overall, the contributions of this paper are as follows:

• Pre-training Transformer models with mixtures of various function classes for context learning and describing the characteristics of model selection behavior;
• Studying the behavior of pre-trained Transformer models on functions "inconsistent" with the function classes in the pre-training data;
• Strong evidence has shown that models can perform model selection within the pre-trained function classes during context learning with almost no additional statistical cost, but there is also limited evidence that the model's context learning behavior can extend beyond the scope of its pre-training data.

The researchers believe that this may be good news for safety, at least the model will not "do whatever it wants."

However, some have pointed out that the model used in this paper may not be suitable— the "GPT-2 scale" implies that the model in this paper probably has about 1.5 billion parameters, which indeed makes it difficult to generalize.

Next, let's take a look at the details of the paper.

Model Selection Phenomenon

When pre-training on mixtures of data from different function classes, a problem arises: how does the model choose between different function classes when it sees context samples supported by the pre-training mixture?

The researchers found that the model makes the best (or near-best) predictions after seeing context samples belonging to function classes in the pre-training data mixture. They also observed the model's performance on functions not belonging to any single constituent function class and then discussed some functions completely unrelated to all pre-training data in Section 4.

They started their investigation with linear functions, which have received widespread attention in the context learning field. Last year, a paper by Percy Liang and others at Stanford University titled "What Can Transformers Learn In-Context? A Case Study of Simple Function Classes" demonstrated that Transformers pre-trained on linear functions perform near-optimally when learning from new linear functions.

They specifically considered two models: one trained on dense linear functions (all coefficients of the linear model are non-zero), and the other trained on sparse linear functions (only 2 out of 20 coefficients are non-zero). On new dense and sparse linear functions, each model's performance is comparable to linear regression and Lasso regression, respectively. Additionally, the researchers compared these two models with models pre-trained on mixtures of sparse and dense linear functions.

As shown in Figure 1, the model's performance in context learning from a

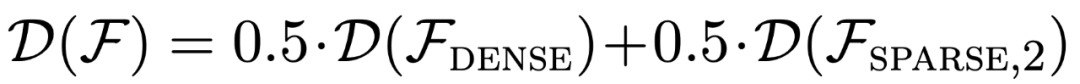
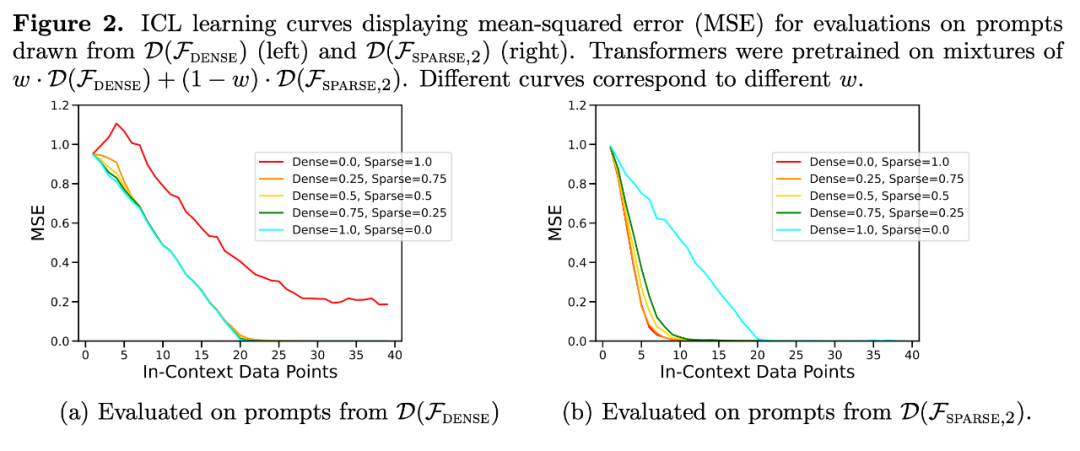
mixture is similar to a model pre-trained only on one function class. Since the performance of the pre-trained model on the mixture is similar to the theoretically optimal model by Garg et al.[4], the researchers inferred that the model is also close to optimal. The ICL learning curve in Figure 2 indicates that this context model selection ability is relatively consistent with the number of context examples provided. Figure 2 also shows that for specific function classes, various non-trivial weights are used

.

The ICL learning curve of the pre-training data mixture almost matches the optimal baseline sample complexity. The observed bias is small, and with an increase in the number of ICL samples, the bias rapidly decreases, consistent with the behavior of a point on the ICL learning curve in Figure 1.

Figure 2 also indicates that the ICL generalization of the Transformer model will be affected by out-of-distribution influences. Although both dense linear class and sparse linear class are linear functions, it can be seen that the performance of the red curve in Figure 2a (corresponding to the Transformer pre-trained only on sparse linear functions and evaluated on dense linear data) is poor, and vice versa, the performance of the brown curve in Figure 2b is also poor. Similar performance was observed by the researchers in other non-linear function classes as well.

Returning to the experiments in Figure 1, the error is plotted as a function of the number of non-zero coefficients over the entire possible range, and the results show that the model pre-processed on the mixture at w = .5

performs equally well throughout the process as the model pre-processed on the mixture (i.e., w = 0 and w = 1) (Figure 3a). This indicates that the model is able to make model selections to choose whether to use the knowledge of one base function class in the pre-trained mixture or the knowledge of another base function class for prediction.

In fact, Figure 3b shows that when the samples provided in the context come from very sparse or very dense functions, the predicted results are almost identical to the predicted results of the model pre-trained using only sparse data or only dense data. However, between the two, when the number of non-zero coefficients ≈ 4, the mixed predicted results deviate from the pure dense or pure sparse pre-trained Transformer predicted results.

This indicates that the model pre-trained on the mixture does not simply choose a single function class for prediction but predicts results that lie between the two.

Limitations of Model Selection Ability

Next, the researchers examined the model's ICL generalization ability from two directions. First, they tested the model's ICL performance on functions never seen during training; second, they evaluated the model's ICL performance on extreme versions of functions seen during pre-training.

In both cases, the study found little evidence of out-of-distribution generalization. Predictions become unstable when the functions differ significantly from those seen during pre-training; however, the model can approximate well when the functions are close enough to the pre-training data.

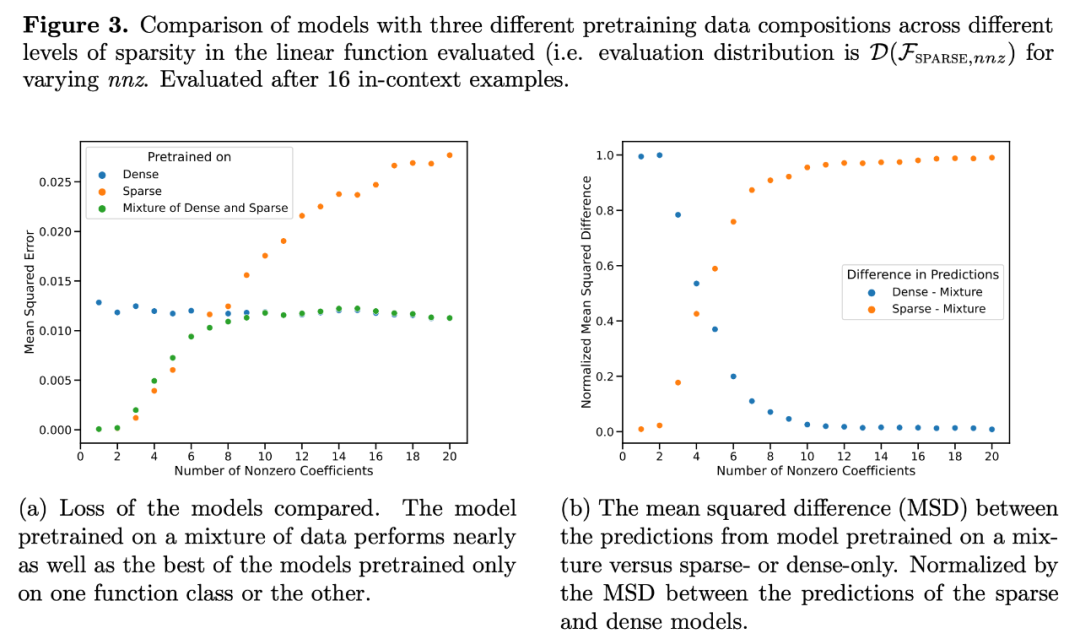
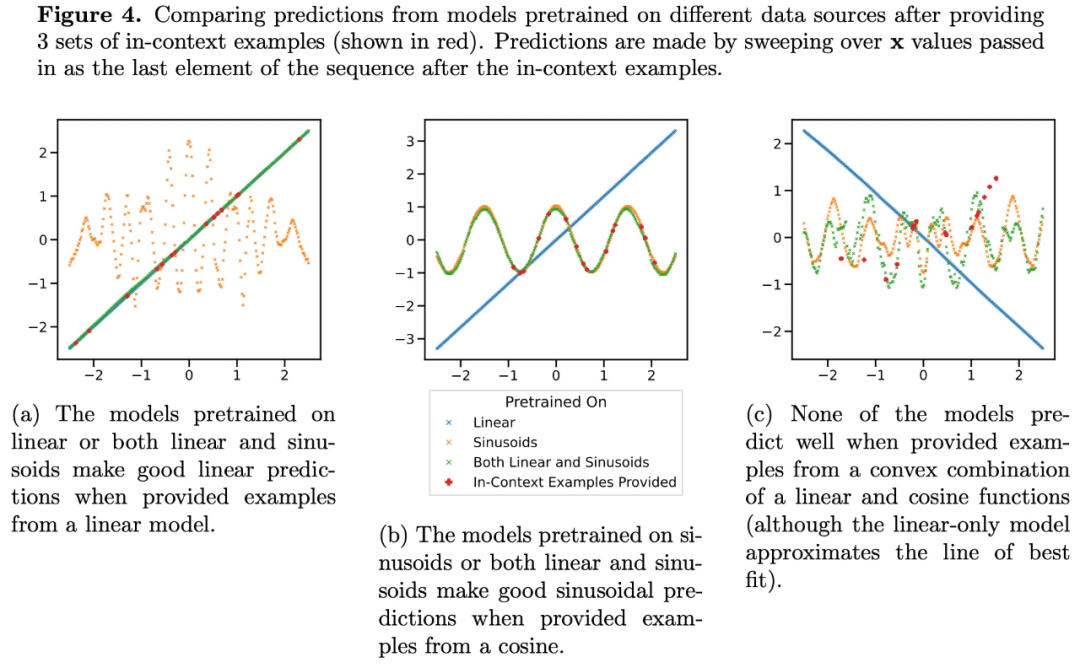
Figure 3a shows that the Transformer's predictions at moderate sparse levels (nnz = 3 to 7) are dissimilar to any predictions provided during pre-training for either function class, but lie between the two. Therefore, it may be assumed that the model has some inductive bias that allows it to combine the knowledge of the pre-trained function classes in a non-trivial way. To test this assumption in the context of clearly disjoint function classes, the researchers explored the model's ability to perform ICL on linear functions, sine curves, and their convex combinations. They focused on the one-dimensional case to simplify the evaluation and visualization of non-linear function classes.

Figure 4 shows that while the model pre-trained on a mixture of linear functions and sine curves (i.e.,

) can make good predictions for either of these two functions, it cannot fit the convex combination function of the two. This indicates that the linear function interpolation phenomenon shown in Figure 3b is not a generalizable inductive bias of Transformer context learning. However, it continues to support a narrower hypothesis that the model can choose the best function class for prediction when the context samples are close to the function classes learned during pre-training.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。