Analysis of Security Vulnerabilities in GG18/GG20 Protocol

Author: Max, Safeheron

Background

Recently, the Fireblocks team disclosed a 0-day vulnerability in the GG18, GG20, and Lindel 17 MPC protocols, which allows attackers to extract the real key behind a set of MPC private key shards.

Before disclosing this issue, the Fireblocks team contacted Safeheron and engaged in active communication. Safeheron's open-source GG18/GG20 MPC protocol strictly follows the content of the paper. If this version of the open-source algorithm is used, it may be vulnerable to similar attacks. Before the vulnerability was disclosed, Safeheron had already fixed the vulnerabilities in the open-source project, and the Fireblocks team also assisted in confirming the effectiveness of the patch.

The Fireblocks team constructed a POC using Safeheron's open-source GG18/GG20 protocol based on C++ implementation to demonstrate and help the community understand the vulnerability.

The commercial version of Safeheron's GG18/GG20 MPC protocol in the business edition introduces relevant zero-knowledge proofs from CMP20/CGGMP21, and therefore is not affected by this vulnerability.

Vulnerability Scope

This article focuses on the vulnerability's impact on GG18 and GG20. For the GG18/GG20 protocols, attackers can complete the attack in the MPC signature phase by constructing a special Paillier key, allowing them to resolve the private key shards of other participants through a limited number of signatures.

The scope of this vulnerability is quite extensive, as it affects the security assumptions of the MPC protocol, and therefore almost all mainstream open-source GG18/GG20 protocol implementations are affected by this vulnerability.

Vulnerability Principle

How can an MPC protocol be attacked? Common MPC protocols are provably secure under security assumptions, so attacks on MPC protocols often focus on the security assumptions on which the protocol relies. Security assumptions are like the foundation of the MPC protocol building. If the security assumptions are no longer valid, the entire MPC protocol will be affected.

Taking GG18/GG20 as an example, this MPC protocol relies on the security of the Paillier homomorphic encryption algorithm. The Paillier homomorphic encryption algorithm is designed based on the difficulty of the composite residue class problem and is a widely used homomorphic encryption algorithm that satisfies addition operations. This vulnerability targets the construction of the Paillier homomorphic key, progressively compromising the $$MtA$$ protocol and related zero-knowledge proof protocols, ultimately leading to an effective attack.

The core logic of the entire attack is as follows:

(1) In the KeyGen sub-protocol phase, the attacker constructs an insecure homomorphic key.
(2) In the Sign sub-protocol phase:
(a) In the pairwise execution of the $$MTA$$ protocol, such as the $$MtA(k,x)$$ and $$MtA(k,\gamma)$$ protocols, the attacker constructs an illegal $$k$$ value based on their own insecure homomorphic key.
(b) Using the properties of the insecure homomorphic key, the attacker constructs a malicious zero-knowledge proof to deceive other participants through verification.
(c) The attacker completes the signature with the victim and records the process's $$\mu$$.
(3) Repeating the Sign sub-protocol several times to calculate the opponent's private key shard based on the Chinese Remainder Theorem.

Vulnerability Attack Method

In this section, we will detail the attack's specifics. In the general MPC threshold multi-signature scenario, there are multiple participants, and each pair of participants can launch an attack, and the attack method is completely the same.

To facilitate the explanation of the attack method, let's assume that the MPC wallet is jointly created and used by three parties: Party A, Party B, and Party C, each managing their own private key shards $$x_A$$, $$x_B$$, and $$x_C$$, respectively. Using this vulnerability, Party A can attack Party B and Party C to obtain the opponent's private key shard. In this section, we will use "Party A attempts to attack Party B" as an example to explain how to extract Party B's private key shard $$x_B$$. (Party A can extract Party C's private key shard $$x_C$$ in the same way, which will not be further elaborated here.)

4.1 Preparation Phase - Constructing an Insecure Homomorphic Key

The first attack occurs during the execution of the KeyGen sub-protocol, which we can call the attack preparation phase. In the attack preparation phase, the attacker Party A successfully constructs an insecure Paillier homomorphic key.

The process of normally constructing a homomorphic key is as follows:

Randomly select secure prime numbers $$p, q \in \{0,1\}^{1024}$$
Calculate
$$ N_A = p * q$$
$$\lambda_A = (p-1)*(q-1)$$

The process of Party A constructing the homomorphic key is as follows:

Randomly select primes $$(p_1, p_2, …, p_{16}, q)$$, where $$p_i$$ are distinct small primes, and $$q$$ is a large prime
Calculate
$$ N_A = \Pi_i{p_i} * q$$, where the length of $$N_A$$ is 2048 bits
$$\lambda_A = \Pi_i(p_i-1)*(q-1)$$

We can see that the Paillier public key $$N_A$$ constructed by the attacker Party A contains a large number of small factors. Can the insecure Paillier key constructed by Party A deceive Party B? After all, a zero-knowledge proof needs to be constructed for Party B to verify.

Carefully observing the KeyGen protocol in the GG18/GG20 as shown in the above figure, it can be found that only a $$Square-Free$$ zero-knowledge proof is required here. Since the Paillier homomorphic public key $$N_A$$ constructed by the attacker Party A only contains distinct prime factors, this construction method can obviously pass the $$Square-Free$$ zero-knowledge proof.

4.2 Attack Phase: Sign Sub-Protocol

Note that the attack needs to successfully execute the Sign sub-protocol 16 times. Let's assume that the current execution is the $i$-th time of the Sign sub-protocol.
In the Sign sub-protocol, the first few rounds require running the $$MtA$$ protocol, referring to GG18 (https://eprint.iacr.org/2019/114.pdf) Section 4.2.

$$ MtA(k_A, \gamma_B) : \alpha_A + \beta_B \leftarrow k_A * \gamma_B$$
$$ MtA(k_A, x_B) : \mu_A + \nu_B \leftarrow k_A * x_B$$

The normal calculation process is as follows:

Randomly select $$k_A \in Zq$$
Calculate $$Enc(k_A)$$
Execute the $$MtA$$ protocol
$$ MtA(k_A, \gamma_B) : \alpha_A + \beta_B \leftarrow k_A * \gamma_B$$
$$ MtA(k_A, x_B) : \mu_A + \nu_B \leftarrow k_A * x_B$$
Generate a zero-knowledge proof about the ciphertext $$Enc(k_A)$$ of the random number $$k_A$$. Refer to GG18 (https://eprint.iacr.org/2019/114.pdf) Section A.1 Range Proof
Subsequently, complete the MPC Sign sub-protocol normally

The attacker's calculation process is as follows:

Construct a special $$k_A$$ value
Use the specially constructed $$k_A$$ value to execute the $$MtA$$ protocol normally
Construct a malicious zero-knowledge proof to deceive
Subsequently, complete the MPC Sign sub-protocol normally

Next, let's introduce the specific operational method.

Constructing a Special $$k_A$$ Value

The attacker does not use a random value but, in the $i$-th MPC Sign sub-protocol, constructs $$k_A$$ as follows.
$$ k_A = N_A / p_i $$
Note that this specially constructed $$k_A \gg q^3$$, and under normal circumstances, it is already impossible to pass the expected zero-knowledge proof. Here, $$q$$ is the order of the elliptic curve.

Constructing a Zero-Knowledge Proof

The GG18 protocol requires the attacker to provide a valid zero-knowledge proof during the $$MtA$$ execution phase, referring to GG18 (https://eprint.iacr.org/2019/114.pdf) Section A.1 Range Proof. This zero-knowledge proof can prove:

Witness: $k_A' = 0 \ne k_A$, other random numbers
Statement: $Enc_{N_A}(k_A)$ is the encrypted ciphertext of $$k_A'$$ and satisfies $$k_A \in (-q^3, q^3) $$

Note that the above is an illegal Statement because:

$$Enc_{N_A}(k_A)$$ is not the encrypted ciphertext of $$k_A'=0$$
$$k_A \gg q^3$$

Under normal circumstances, the Range Proof at this point in the GG18 protocol is completely valid, and it is difficult for the attacker to construct a zero-knowledge proof that allows this Statement to pass verification.

So, how does the attacker Party A overcome this obstacle? This is where the insecure Paillier key $$N_A$$ constructed by the attacker Party A in the KeyGen protocol phase comes into play. Because of the insecure Paillier key, there is an opportunity to construct a malicious zero-knowledge proof.

Description of the Zero-Knowledge Proof Protocol in the GG18/GG20 Protocol:

In the Verifier's verification process, the most important part is satisfying the identity constraint of the ciphertext (highlighted in red):

$$ u = \Gamma^s s^N c^{-e} \pmod {N^2} $$
The attack technique involves constructing a reasonable challenge value $$e = Hash(…, w, )$$ that satisfies: $$e \pmod {p_i} = 0$$
Since $$c = (1+N_A)^k_A * \rho^N_A \mod (N_A^2)$$, $$k_A = N_A/p_i$$
$$\begin{align*}
c^e &= ((1+N_A)^k_A * \rho^N_A)^e &\mod (N_A^2) \\
&= (1+N_A)^{ek_A} * \rho^{eN_A} &\mod (N_A^2) \\
&= (1+N_A)^{bp_i * N_A/p_i} * \rho^{eN_A} &\mod (N_A^2) \\
&= \rho^{e_AN} &\mod (N_A^2) \\
&= Enc_{N_A}(0)^e &\mod (N_A^2) \\
\end{align*}$$

Here, $$c$$ is "transformed" into the ciphertext of $$k_A'=0$$, successfully constructing the zero-knowledge proof.

Note that by iteratively brute-forcing $$\gamma$$ in the construction process, continually adding 1, and updating $$w$$, it is possible to satisfy $$e \pmod {p_i} = 0$$. Since the modulus $p_i$ is a small prime, it is entirely possible to successfully brute-force iterate.

Calculating the Modulus $$p_i$$ Residue of Party B's Private Key Shard

The attacker completes the Sign sub-protocol with the victim and additionally records the value $$\mu_A$$ in the $$MtA$$ protocol.
$$ \mu_A = k_A * x_B + \nu_B \pmod {N_A}$$
Considering the latest version of the GG18 paper, it is known that $$\nu_B \le q^5$$,
$$ \mu_A = Dec_{N_A}(Enc_{N_A}(k_A * x_B + v_B))$$
$$\begin{align*}
\mu_A - (\mu_A \mod (N_A/p_i)) =& Dec_{N_A}(Enc_{N_A}(k_A * x_B + \nu_B)) - (Dec_{N_A}(Enc_{N_A}(k_A * x_B + \nu_B)) \mod (N_A/p_i))\\
=& (x_B \mod p_i) * (N_A/p_i) + \nu_B - \nu_B \\
=& (x_B \mod p_i) * (N_A/p_i)
\end{align*}$$

It can be seen that:

$$x_B \pmod {p_i} = (\mu_A - (\mu_A \mod (N_A/p_i)))/(N_A/p_i) $$
Let $$a_i = (\mu_A - (\mu_A \mod (N_A/p_i)))/(N_A/p_i) $$

Noting that all the parameters on the right-hand side of the equation are known to the attacker, the attacker can calculate $$a_i$$
Thus, we have: $$x_B = a_i \pmod {p_i}$$

4.3 Conclusion Phase: Calculating the Victim's Private Key Shard

After successfully running the Sign sub-protocol 16 times, we obtain:

$$ x_B = a_1 \pmod {p_1}$$
$$ x_B = a_2 \pmod {p_2}$$
$$ … $$
$$ x_B = a_{16} \pmod {p_{16}}$$

Since $$p_1 * p_2 *… * p_{16} > q$$, according to the Chinese Remainder Theorem, the attacker Party A can calculate Party B's private key shard $$x_B$$. The attack is successful.

4.4 Attack Effect

The GG18 paper has two implementation versions, the revised version and the old version, and the attack effect differs for different versions.

-In the revised version of the paper, the $$MtA$$ protocol uses $$\beta_B q^5$$ (corresponding to the previous $$\nu_B$$), and using the above attack method, the attacker can extract the victim's private key shard with 16 signatures.
-In the old version of the paper, the $$MtA$$ protocol uses $$\beta_B N_A$$ (corresponding to the previous $$\nu_B$$), and a variant of the above attack method is needed to carry out the attack. This is not further explained here. Because it requires a large number of guess runs and a large number of signatures, at least on the order of 10^6 signature attempts, for the attacker to potentially extract the victim's private key shard. More precisely, the number of signatures required to successfully extract the opponent's private key shard with a probability of $$\tau^l$$ is: $$\sum_{i=1}^nf_\tau(p_i)$$ times.

Where, $$f_{\tau} (p) = log(1-\tau) / log(1-1/p^2)$$.

The corresponding formula in Fireblocks' paper has a writing error, which has been corrected here.

Note: In the revised version of the GG18 paper, the authors provide many security modification suggestions, so the implementation of this MPC protocol should be based on the revised version.

Real-World Attack Example

The above sections describe the principles and algorithmic attack methods of this vulnerability. So, in a real-world self-hosted wallet application based on MPC, if the MPC protocol used has this vulnerability, how can the attack be carried out?

This vulnerability affects the t/n threshold. For ease of understanding, let's assume that the participants in the MPC Wallet are 2 parties, Party A and Party B, and the signature threshold is 2/2. Party A's private key shard is held by the user and managed and used through a mobile app provided by the wallet provider. Party B's private key shard is held by the wallet provider and stored and used in the cloud.

To carry out the attack, the attacker must have the following capabilities:

(1) Understand the implementation logic and mechanism of the wallet provider for creating wallets and initiating transactions
(2) Be able to simulate the wallet provider's app using the MPC protocol to create wallets and sign transactions

The attacker can then launch the attack:

(1) Simulate the app to create a wallet. During wallet creation (corresponding to the KeyGen sub-protocol), construct an insecure homomorphic key for local Party A in the MPC protocol, then use this homomorphic key to create the wallet, while obtaining the local Party A's private key shard $$x_A$$
(2) Simulate the app to use the wallet to sign transactions 16 times as usual (corresponding to the Sign sub-protocol), and each time construct malicious $$k_A$$ and malicious zero-knowledge proofs in the MPC protocol to complete 16 signatures and collect the $$\mu$$ from each signature

After completing the above operations, the attacker can obtain the cloud Party B's private key shard $$x_B$$ corresponding to the created wallet. Since the signature threshold is 2/2, the attacker has obtained the private key shard $$x_A$$ locally and has attacked the protocol to obtain the cloud private key shard $$x_B$$. Thus, the attacker can obtain the real private key $$x$$ corresponding to the wallet using $$x_A$$ and $$x_B$$.

In the above attack scenario, to attack the wallet, the attack must have been initiated at the time of wallet creation and completed by using the wallet to sign multiple times, ultimately obtaining the wallet's private key.

Vulnerability Fix

Throughout the entire attack process, we find that all attacks originate from the attack preparation phase, where the attacker Party A constructs an insecure homomorphic key $$N_A$$, which contains a large number of small factors, leading to subsequent successful attacks.

The vulnerability fix is aimed at this point. In the GG18/GG20 protocol, additional zero-knowledge proofs are added to prevent the appearance of small factors in the homomorphic public key $$N_A$$, thus preventing attacks from the root. For the entire GG18/GG20 protocol, after applying this patch, there are no longer any security issues with the security assumptions, so the protocol remains secure.

Fixing the vulnerability requires adding two zero-knowledge proofs:

-The first zero-knowledge proof is the Blum modulus proof of Paillier, which ensures that the homomorphic public key $$N_A$$ has at most two prime factors, and each prime factor satisfies specific properties.
-The second zero-knowledge proof is the small factor proof, ensuring that the homomorphic public key $$N_A$$ does not have small prime factors.

The implementation of these two zero-knowledge proofs can refer to CMP20 and CGGMP21 (Sections 6.3 and C.5), which ensure that the Paillier public key $$N$$ has no factors smaller than $$2^{256}$$.

Safeheron has fixed this vulnerability in the open-source algorithm. The specific fix can be found at:

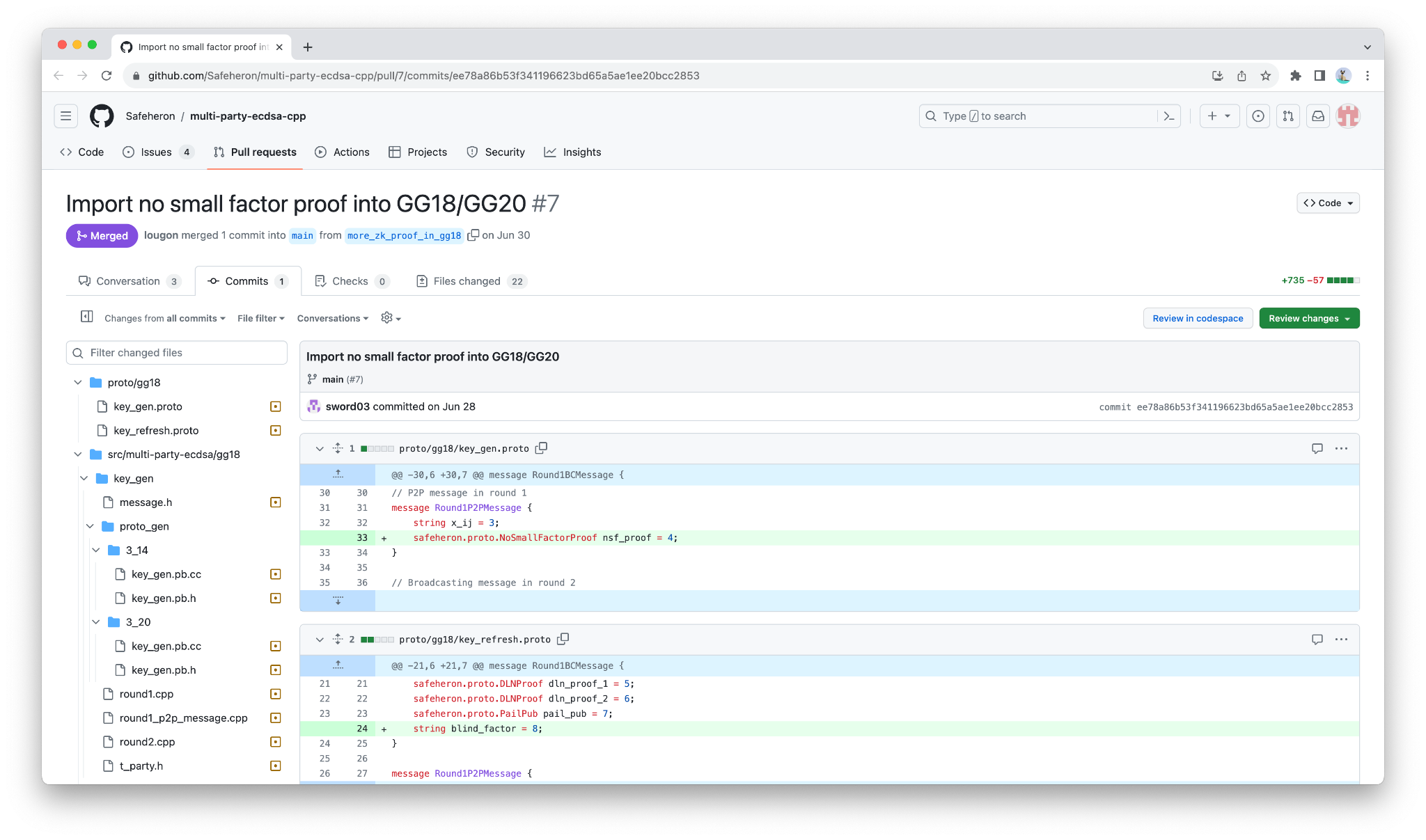https://github.com/Safeheron/multi-party-ecdsa-cpp/pull/7/commits/ee78a86b53f341196623bd65a5ae1ee20bcc2853

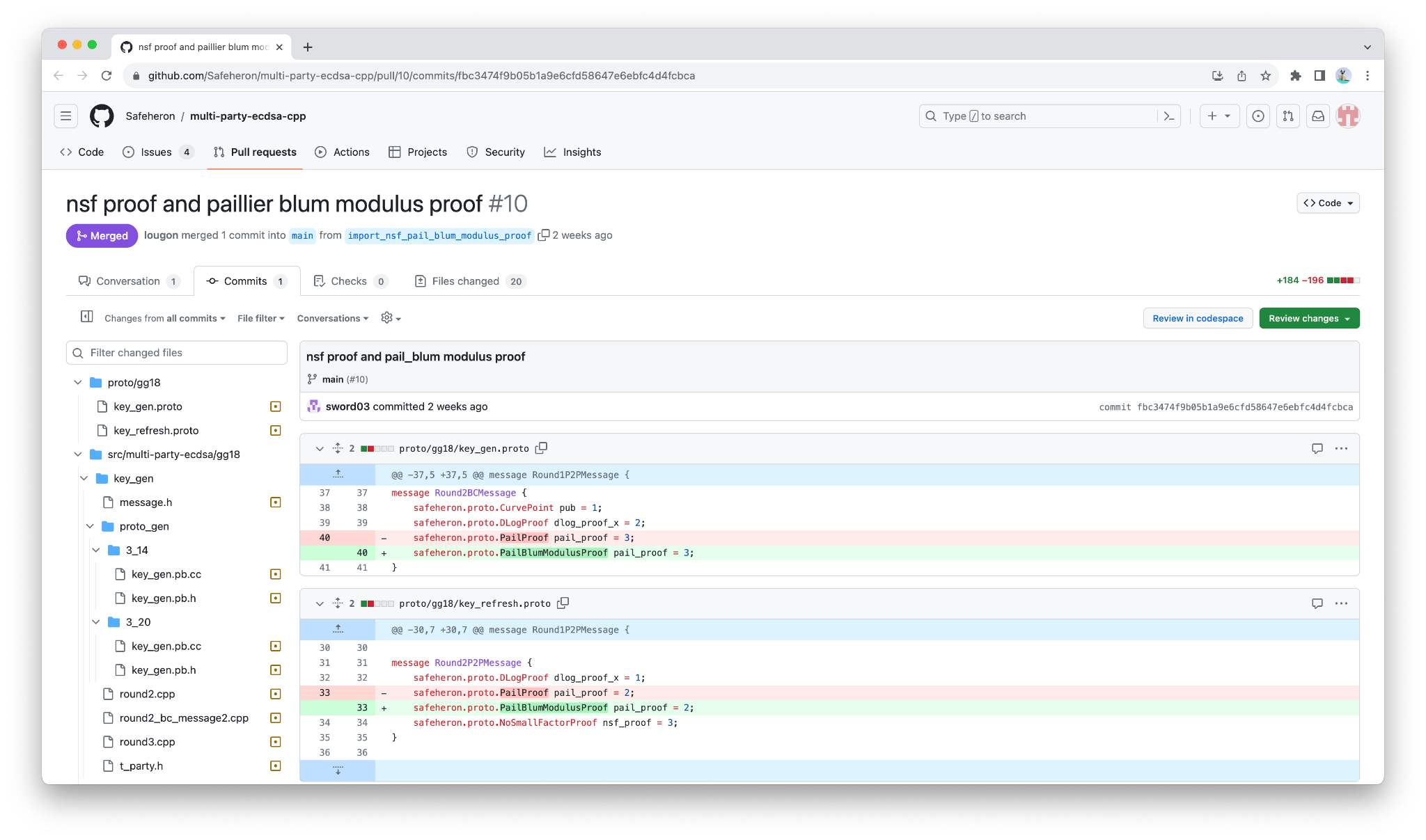https://github.com/Safeheron/multi-party-ecdsa-cpp/pull/10/commits/fbc3474f9b05b1a9e6cfd58647e6ebfc4d4fcbca

Attack Detection

After completing the security upgrade of the MPC protocol, for safety reasons, it is advisable to check historical data to verify if there has been any attack exploiting this vulnerability. Since the exploitation of this vulnerability depends on the construction of an insecure Paillier key, if such attacks have occurred, there will definitely be small factors in the attacker's Paillier public key $$N$$. Therefore, we can analyze whether there are small factors in the Paillier public key $$N$$ of the MPC participants to detect any past attacks.

The specific detection method can use mature large integer factorization algorithm tools to check whether the Paillier modulus $$N$$ has small factors. If small factors are found, there is a possibility of being attacked, and it is recommended to transfer assets as soon as possible and create a new MPC wallet.

Safeheron provides a large integer factorization tool (https://github.com/Safeheron/integer-factorization) for quick batch detection. For the algorithmic principles related to large integer factorization, please refer to Large Integer Factorization Algorithm and Practice (https://mp.weixin.qq.com/s/5FcA0qGXDKFeb_nMatFeWQ).

Conclusion

After understanding the principles and attack methods of this vulnerability, it is not difficult to see that the threshold for exploiting this vulnerability is relatively high. However, in the security industry, facing the unknown and challenging "black forest," we always need to maintain a sense of awe for security.

The responsible security disclosure by the Fireblocks team demonstrates that "security is never fought alone." Safeheron also adheres to open source transparency and places a strong emphasis on technology, and is honored to be able to participate in this security disclosure. Safeheron will work with security partner SlowMist to assist other vendors in the industry in fixing this vulnerability to ensure the security of user assets.

Achieving industry security requires the attention and efforts of every vendor, every security practitioner, and every user. We hope to encourage the industry together.

References
[1] Fireblocks: Practical Key-Extraction Attacks in Leading MPC Wallets (https://github.com/fireblocks-labs/mpc-ecdsa-attacks-23/blob/main/WhitePaper.pdf)
[2] GG18: Fast Multiparty Threshold ECDSA with Fast Trustless Setup (https://eprint.iacr.org/2019/114.pdf)
[3] GG20: One Round Threshold ECDSA with Identifiable Abort (https://eprint.iacr.org/2020/540.pdf)
[4] CGGMP21: UC Non-Interactive, Proactive, Threshold ECDSA with Identifiable Aborts (https://eprint.iacr.org/2021/060.pdf)

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。