Original Title: [Possible futures of the Ethereum protocol, part 4: The Verge]
Author: Vitalik Buterin
Translation: Tia, Techub News
One of the most powerful features of blockchain is that it allows anyone to run a node on their computer and verify that the chain is correct. Even if 95% of the nodes agree to change the rules and start generating blocks according to the new rules, every honest individual running a full node has the ability to reject that chain. Stakeholders who are not part of such a conspiracy will automatically come together and continue to build a chain that follows the old rules, and fully verified users will follow that chain.
This is a key distinction between blockchain and centralized systems. However, to maintain this feature, running a full node needs to be simple enough to ensure that most people have the opportunity to run a node. This applies to both stakers (if stakers do not verify the chain, they are not actually contributing to the execution of the protocol rules) and ordinary users. Nowadays, running a node on a laptop has become possible, but it is still quite difficult. The Verge aims to change this, making the cost of full verification of the chain low enough that every mobile wallet, browser wallet, and even smart watch can become a verification node.
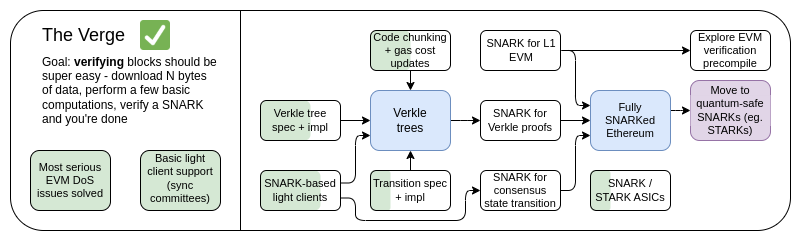
The Verge, 2023 Roadmap
Initially, "Verge" referred to moving Ethereum's state storage to Verkle tree - Verkle tree is a more compact proof tree structure that enables stateless verification of Ethereum blocks. Nodes can verify Ethereum blocks without having any Ethereum state (account balances, contract code, storage…) on their hard drives, but they need to spend hundreds of kilobytes of proof data and a few hundred milliseconds of extra time to verify the proof. Today, the vision of Verge has become grander; Verge aims to achieve maximum resource efficiency in verification of the Ethereum chain, which includes not only stateless verification technology but also using SNARK to verify all Ethereum executions.
In addition to the long-term focus on SNARK verification of the entire chain, another question needs to be considered: Is Verkle tree the best technology? Verkle tree is vulnerable to attacks from quantum computers, so if we replace the current KECCAK Merkle Patricia tree with Verkle tree, we will have to replace the tree again in the future. A natural alternative to Merkle tree is to directly use STARK of Merkle branches in a binary tree. Historically, this has been considered infeasible due to overhead and technical complexity. However, recently we have seen Starkware using circular STARK to prove 1.7 million Poseidon hashes per second, and due to technologies like GKR, it feels like the proof time for more "traditional" hashes is also rapidly improving.
Over the past year, Verge has become more open and has shown rich possibilities.
The Verge: Key Goals
Stateless client: Fully verified clients and staking nodes do not need more than a few GB of storage space.
In the future, it will be possible to perform chain verification (consensus and execution) on smart watches. That is, as long as some data is downloaded and SNARK is verified, it can be completed.
Stateless Verification: Verkle or STARK
What problem are we trying to solve?
Today, Ethereum clients need to store hundreds of GB of state data to verify blocks, and this amount is increasing every year. The original state data grows by about 30 GB each year, and various clients must store some additional data on top of it to effectively update the trie.
This reduces the number of users who can run fully verified Ethereum nodes: although as long as there is a sufficiently large hard drive, one can store all Ethereum states or even history for years at any time, the computers that people typically buy often only have a few hundred GB of storage space. The size of the state also creates significant resistance in the process of setting up a node for the first time: nodes need to download the entire state, which can take hours or even days. This creates various chain reactions. For example, it makes it more difficult for stakers to upgrade their staking setups. Technically, this can be done without downtime - starting a new client, waiting for it to sync, then shutting down the old client and transferring the keys - but in practice, this technique is complex.
What is Stateless Verification and How Does It Work?
Stateless verification is a technology that allows nodes to verify blocks without having the complete state. Instead, each block comes with a witness, which includes (i) the value (e.g., code, balance, storage) at specific locations in the state that the block will access, and (ii) the cryptographic proof that these values are correct.
In practice, implementing stateless verification requires changes to the Ethereum state tree structure. This is because the current Merkle Patricia tree is extremely unfriendly for implementing any cryptographic proof scheme, especially in the worst case. This is true for both the "raw" Merkle branches and the possibility of "wrapping" Merkle branches in STARK. The key difficulties stem from two weaknesses of MPT:
It is a 16-ary tree (i.e., each node has 16 children). This means that on average, the proof in a tree of size N has
32 * (16 - 1) * log16(N) = 120 * log2(N)bytes, or about 3840 bytes in a tree of 2^32 items. Using a binary tree, you only need32 * (2 - 1) * log2(N) = 32 * log2(N)bytes, or about 1024 bytes.The code is not Merkleized. This means that proving access to any account code requires providing the entire code, up to 24000 bytes.
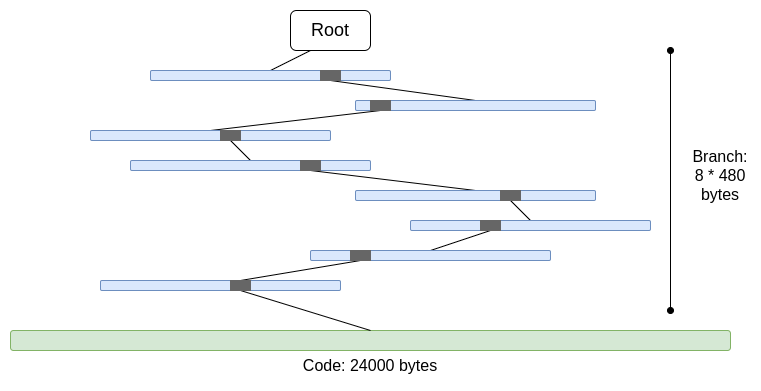
The worst-case scenario we can calculate is as follows:
30,000,000 gas / 2,400 ("cold" account read cost) * (5 * 480 + 24,000) = 330,000,000 bytes
The branch cost decreases slightly (5 * 480 instead of 8 * 480), because when there are more branches, the top of the branches will repeat. But even so, this means that the amount of data downloaded within a slot is completely impractical. If we try to wrap it in STARK, we will encounter two problems: (i) KECCAK is relatively unfavorable for STARK, (ii) 330 MB of data means we have to prove 5 million calls to the KECCAK round function, which is too much for all hardware except the most powerful consumer-grade hardware, even if we can make the STARK proof of KECCAK more efficient.
If we simply replace the 16-ary tree with a binary tree and additionally Merkleize the code, then the worst-case scenario is about 14 bytes (14 is ~2 (14) 30,000,000 / 2,400 * 32 * (32 - 14 + 8) = 10,400,000 bits of redundancy subtracted from the branches, where 8 is the proof length of leaf nodes in the block). Note that this requires changing the gas cost to charge for accessing each individual code block; EIP-4762 does just that. 10.4 MB is much better, but for many nodes, the amount of data downloaded within a slot is still too much. So we need to introduce some more powerful technologies. For this, there are two leading solutions: Verkle tree and STARKed binary hash tree.
Verkle trees
Verkle tree uses elliptic curve-based vector commitments to create shorter proofs. The key point is that regardless of the width of the tree, the proof portion corresponding to each parent-child relationship is only 32 bytes. The only limitation on tree width is that if the tree is too wide, the computational efficiency of the proof will decrease. Ethereum proposes an implementation width of 256.
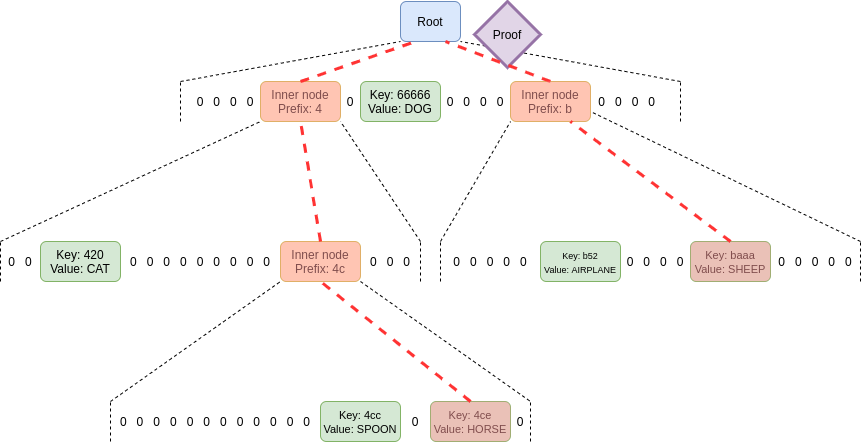
Thus, the size of a single branch in the proof is 32 * log256(N) = 4 * log2(N) bytes. Therefore, the theoretical maximum proof size is approximately 30,000,000 / 2,400 * 32 * (32 - 14 + 8) / 8 = 1,300,000 bytes (the actual calculation may vary slightly due to uneven distribution of state blocks, but this is fine as a preliminary approximation).
It is also important to note that in all the examples above, this "worst-case" scenario is not entirely the worst case: a worse case would be if an attacker deliberately "mines" two addresses, creating a long common prefix in the tree, and reads from one of those addresses, which could extend the worst-case branch length by about 2 times. But even with this caveat, Verkle tree allows us to achieve a worst-case proof of about 2.6 MB, which is roughly equivalent to today's worst-case calldata.
We also leverage this warning to do another thing: we make accessing "adjacent" storage very cheap: either many code blocks of the same contract or adjacent storage slots. EIP-4762 provides a definition of adjacency, and adjacent access only costs 200 gas. For adjacent access, the worst-case proof size becomes 30,000,000 / 200 * 32 = 4,800,800 bytes, which is still roughly within tolerance. If we want to lower this value for security reasons, we can slightly increase the cost of adjacent access.
STARK-based Binary Hash Tree
The technology here is quite straightforward: you create a binary tree, extract the maximum 10.4 MB proof needed for the proof block, and replace that proof with the STARK of that proof. This way, the proof itself only contains the data to be proven, plus a fixed overhead of about 100-300 kB for the actual STARK.
The main challenge here is the verification time. We can perform calculations similar to those above, but we calculate hash values instead of byte counts. A 10.4 MB block means 330,000 hash values. If we add the possibility of an attacker "mining" addresses with a long common prefix in the tree, then the real worst case is about 660,000 hash values. Therefore, if we can verify about 200,000 hash values per second, that would be fine.
These numbers have already been achieved on consumer-grade laptops using the Poseidon hash function, which is designed for STARK friendliness. However, Poseidon is relatively immature, so many people are still skeptical about its security. Therefore, there are two realistic paths forward:
Conduct rapid security analysis of Poseidon and familiarize with how to deploy it on L1.
Use more "conservative" hash functions, such as SHA256 or BLAKE.
At the time of writing, Starkware's circular STARK prover can only prove about 10-30k hash values per second on consumer-grade laptops when proving conservative hash functions. However, STARK technology is rapidly improving. Even today, GKR-based technology is expected to raise this to around 100-200k.
Use Cases for Witnesses Beyond Block Verification
In addition to block verification, there are three other key use cases for more efficient stateless verification:
Memory Pool: When transactions are broadcast, nodes in the p2p network need to verify whether the transaction is valid before rebroadcasting. Currently, verification involves checking signatures, ensuring sufficient balance, and verifying the randomness. In the future (for example, using native account abstraction like EIP-7701), this may involve running some EVM code that accesses some state. If the node is stateless, the transaction will need to come with a proof of the state object.
Inclusion Lists: This is a proposed feature that allows (potentially smaller and less complex) proof-of-stake validators to enforce that the next block includes a transaction, regardless of the (potentially larger and more complex) block builder's wishes. This would reduce the ability of powerful participants to manipulate the blockchain by delaying transactions. However, this requires validators to have a way to verify the validity of transactions in the inclusion list.
Light Clients: If we want users to access the blockchain through wallets (like Metamask, Rainbow, Rabby…) without trusting centralized participants, they need to run light clients (like Helios). The core Helios module provides users with verified state roots. However, to achieve a completely trustless experience, users need to provide proofs for every RPC call they make (for example, for eth_call requests, users need to provide proofs for all states accessed during the call).
All these use cases share a commonality in that they require a considerable amount of proof, but each proof is small. Therefore, STARK proofs are not practical for them; instead, directly using Merkle branches is the most realistic approach. Another advantage of Merkle branches is that they are updatable: given a proof of a state object X rooted in block B, if you receive a sub-block B2 with its witness, you can update that proof to root it in block B2. Verkle proofs themselves are also updatable.
Connections to Existing Research
Verkle tree: https://vitalik.eth.limo/general/2021/06/18/verkle.html
John Kuszmaul's original Verkle tree paper: https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf
Starkware proof data: https://x.com/StarkWareLtd/status/1807776563188162562
Poseidon2 paper: https://eprint.iacr.org/2023/323
Ajtai (lattice-hardness-based alternative fast hash function): https://www.wisdom.weizmann.ac.il/~oded/COL/cfh.pdf
Verkle.info: https://verkle.info/
What Remains to Be Done? What Are the Trade-offs?
The main work remaining to be done includes:
More analysis of the consequences of EIP-4762 (stateless gas cost changes).
More work is needed to complete and test the transition program, which is a significant part of the complexity of the stateless EIP.
More security analysis of Poseidon, Ajtai, and other "STARK-friendly" hash functions.
Further development of ultra-efficient STARK protocols for "conservative" (or "traditional") hash functions, such as ideas based on Binius or GKR.
We will soon reach a decision point, choosing among the following three options: (i) Verkle tree, (ii) STARK-friendly hash functions, and (iii) conservative hash functions. Their properties can be roughly summarized in the table below:
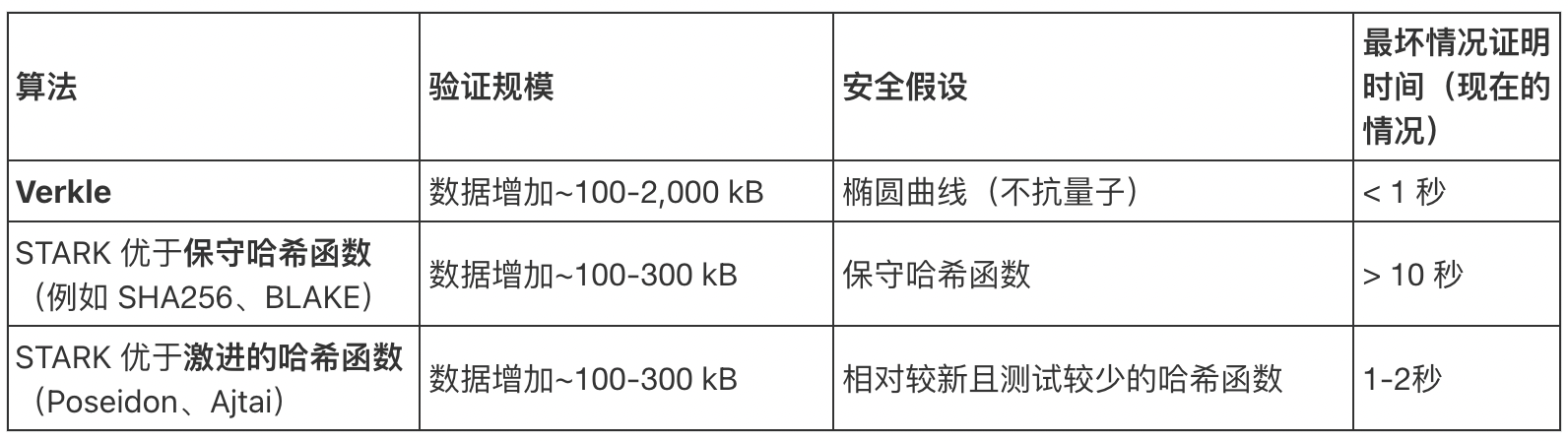
In addition to these "overall numbers," there are also other important considerations:
Today, the Verkle tree code is quite mature. Using any code other than Verkle would actually delay deployment, likely resulting in a hard fork. This is acceptable, especially if we need additional time for hash function analysis or prover implementation, and if we have other important features we want to include in Ethereum sooner.
Using hashes to update the state root is faster than using the Verkle tree. This means that hash-based methods can shorten the synchronization time for full nodes.
Verkle trees have interesting witness update properties - Verkle tree witnesses are updatable. This property is very useful for memory pools, inclusion lists, and other use cases, and it may also help improve implementation efficiency: if the state object has been updated, you can even update the penultimate witness without reading the last level.
Verkle trees are harder to prove via SNARKs. If we want to reduce the proof size to a few kilobytes, Verkle proofs present some challenges. This is because the verification of Verkle proofs introduces a large number of 256-bit operations, which requires the proof system to either have a lot of overhead or have custom internal constructs where the 256-bit parts are used for Verkle proofs. This is not a problem for statelessness itself, but it will create more difficulties later on.
If we want to achieve Verkle witness updatability in a quantum-safe and reasonably efficient manner, another possible approach is lattice-based Merkle trees.
If the proof system is not efficient enough in the worst case, we can use another "unexpected" approach to compensate for this shortcoming, which is multidimensional gas: setting separate gas limits for (i) call data, (ii) computation, (iii) state access, and possibly other different resources. Multidimensional gas increases complexity, but in exchange, it more strictly limits the ratio between average and worst-case scenarios. With multidimensional gas, the theoretical maximum number of branches that need to be proven could potentially reduce from 30,000,000 / 2400 = 12,500 to 3000. In this case, even today's BLAKE3 would suffice, without further improvements to the proof.
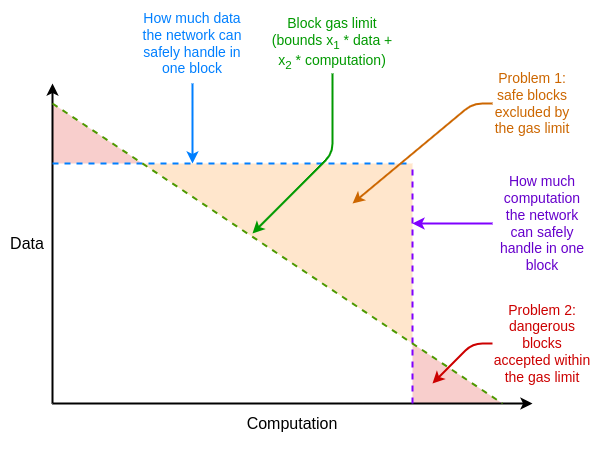
Another "unexpected" proposal is to delay the calculation of the state root until after the block's slot. This would give us a full 12 seconds to compute the state root, meaning that even in the most extreme cases, only ~60,000 hashes/second of proof time would be sufficient, which again puts us within the range of BLAKE3, barely enough.
The downside of this approach is that it increases light client latency, but there are more clever versions of this technique that can reduce the delay to proof generation delay. For example, as long as any node generates a proof, it can be broadcast over the network without waiting for the next block.
How does it interact with other parts of the roadmap?
Addressing the stateless issue greatly enhances the convenience of solo staking. If technologies that can lower the minimum balance for solo staking (such as Orbit SSF or application layer strategies like Squad Staking) become available, it will become even more valuable.
If EOF is introduced simultaneously, multidimensional gas will become easier. This is because one key complexity of executing multidimensional gas lies in handling sub-calls that do not pass on all gas from the parent call, while EOF can trivialize this issue by simply making such sub-calls illegal (and native account abstraction will provide an in-protocol alternative for the current partial gas sub-calls).
Another important synergy is between stateless verification and historical expiration. Nowadays, clients must store nearly 1TB of historical data; this data is several times larger than the state. Even if the client is stateless, unless we can alleviate the client's responsibility to store history, the dream of having almost no storage client cannot be realized. The first step in this regard is EIP-4444, which also implies storing historical data in torrent or Portal networks.
Validity Proof of EVM Execution
What problem are we trying to solve?
The long-term goal of Ethereum block validation is clear: you should be able to verify Ethereum blocks by (i) downloading the block, or even just downloading a small part of the block (using data availability sampling); (ii) validating a small proof. This would be a resource-efficient operation that could be performed on mobile clients, browser wallets, or even (without the data availability part) on another chain.
To achieve this, there needs to be (i) a consensus layer (i.e., proof of stake) and (ii) an execution layer (i.e., EVM) with SNARK or STARK proofs. The former is a challenge in itself and should be addressed in the process of further improving the consensus layer (e.g., single slot finality). The latter requires proofs of EVM execution.
What is the validity proof of EVM execution and how does it work?
In the Ethereum specification, the EVM is defined as a state transition function: you have some pre-state S, a block B, and you are computing a post-state S' = STF(S, B). If a user is using a light client, they do not have S and S' or even all of B; instead, they have a pre-state root R, a post-state root R', and a block hash H. The complete statement that needs to be proven is roughly as follows:
Public inputs: pre-state root
R, post-state rootR', block hashHPrivate inputs: block body
B, objectsQin the state accessed by the block, the same objectsQ'after executing the block, state proof (e.g., Merkle branch)PClaim 1:
Pis a valid proof containing the following part of the state:QRClaim 2: If
STFis run onQ, then (i) the execution only accesses the internal objectsQ, (ii) the block is valid, and (iii) the result isQ'Claim 3: If you recalculate the new state root using the information in
P, you will getR'
If this is the case, you can have a lightweight client that fully verifies Ethereum EVM execution. This already makes the resource usage of the client very low. To achieve a truly fully verified Ethereum client, you would also need to do the same for the consensus side.
The implementation of validity proofs for EVM computation already exists and is widely used in layer 2. However, there is still much work to be done to make EVM validity proofs applicable to L1.
What are the connections to existing research?
EF PSE ZK-EVM (now deprecated as there are better options): https://github.com/privacy-scaling-explorations/zkevm-circuits
Zeth works by compiling the EVM into the RISC-0 ZK-VM: https://github.com/risc0/zeth
ZK-EVM formal verification project: https://verified-zkevm.org/
What remains to be done? What are the trade-offs?
Currently, EVM validity proofs have shortcomings in two areas: security and proof time.
Secure validity proofs involve ensuring that the SNARK indeed verifies EVM computation and that there are no errors in it. The two main techniques for improving security are multi-provers and formal verification. Multi-provers mean having multiple independently written validity proof implementations, just like having multiple clients, and if a sufficiently large subset of these implementations proves a block, the client will accept that block. Formal verification involves using tools commonly used to prove mathematical theorems (e.g., Lean4) to prove that validity proofs only accept inputs that correctly execute the underlying EVM specification (e.g., the EVMK semantics written in Python or the Ethereum Execution Layer Specification EELS).
Sufficiently fast proof times mean that any Ethereum block can be proven in less than 4 seconds. Today, we are still far from this goal, although we are much closer than we were two years ago. To achieve this, we need to make progress in three directions:
- Parallelization - The fastest EVM prover currently can complete a proof for a normal Ethereum block in about 15 seconds. It achieves this by parallelizing across hundreds of GPUs and then aggregating their work at the end. Theoretically, we know exactly how to create an EVM prover that can prove computations in O(log(N)) time: have one GPU execute each step and then create an "aggregation tree":
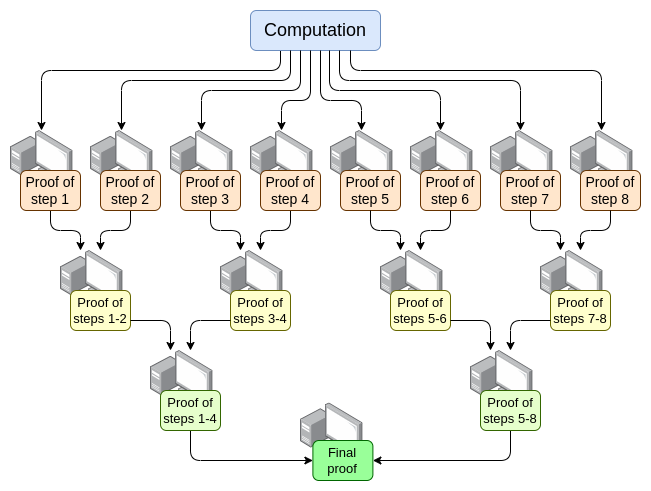
There are challenges in achieving this. Even in the worst-case scenario, where a very large transaction occupies the entire block, the computation cannot be split by transaction; it must be split by opcode (EVM or an underlying VM like RISC-V). One key implementation challenge makes this not entirely straightforward: ensuring that the VM's "memory" is consistent across the different parts of the proof. However, if we can make such recursive proofs, we know that at least the proof latency issue has been resolved, even without improvements on any other axis.
Proof system optimization - New proof systems like Orion, Binius, and GKR may significantly reduce proof times for general computation again.
Other changes to EVM gas costs - Many aspects of the EVM can be optimized to make it more convenient for provers, especially in worst-case scenarios. If an attacker can construct a block that blocks the prover's time for ten minutes, then being able to prove a normal Ethereum block in 4 seconds is not sufficient. The required EVM changes can be roughly divided into two categories:
Gas cost changes - If an operation takes a long time to prove, then even if the computation speed is relatively fast, its gas cost should be high. EIP-7667 is an EIP aimed at the most egregious offenders in this regard: it significantly increases the gas cost of (traditional) hash functions that are publicly available in relatively cheap opcodes and precompiles. To compensate for these increased gas costs, we can lower the gas costs of EVM opcodes that have relatively low proof costs, thereby keeping the average throughput unchanged.
Data structure replacements - In addition to replacing the state tree with alternatives more suitable for STARKs, we also need to replace transaction lists, receipt trees, and other structures that incur high proof costs. Etan Kissling's EIP moves transaction and receipt structures to SSZ (1 2 3) is a step in this direction.
In addition to this, the two "rabbits pulled out of hats" mentioned in the previous section (multidimensional gas and delayed state root) can also help here. However, it is worth noting that, unlike stateless verification, using rabbits pulled out of hats means we have sufficient technology to accomplish what we need to do today, even though complete ZK-EVM verification will require more work (it just requires less work).
One thing not mentioned above is prover hardware: using GPUs, FPGAs, and ASICs to generate proofs faster. Companies like Fabric Cryptography, Cysic, and Accseal are driving this process forward. This will be very valuable for layer 2, but it is unlikely to become a decisive factor for layer 1, as there is a strong desire to maintain a high degree of decentralization in layer 1, meaning that proof generation must be within the capabilities of a significant portion of Ethereum users and should not be limited by the hardware of a single company. Layer 2 can make more aggressive trade-offs.
There is still much work to be done in each of the following areas:
Parallelized proofs require proof systems where different parts of the proof can "share memory" (e.g., lookup tables). We know the techniques to achieve this, but they need to be implemented.
We need to conduct more analysis to determine the ideal gas cost changes to minimize worst-case verification times.
We need to do more work on proof systems.
Possible trade-offs here include:
Security vs. proof time: Proof times can be shortened by choosing more aggressive hash functions, proof systems with more complex or aggressive security assumptions, or other design choices.
Decentralization vs. proof time: The community needs to reach consensus on the "specifications" of the proof hardware it targets. Is it acceptable to require provers to be large entities? Do we want high-end consumer laptops to be able to prove Ethereum blocks in 4 seconds? Somewhere in between?
Degree of breaking backward compatibility: Shortcomings in other areas can be compensated for by making more radical gas cost changes, but this is more likely to disproportionately increase costs for certain applications and force developers to rewrite and redeploy code to maintain economic viability. Similarly, "rabbits in hats" also have their own complexities and downsides.
How does it interact with other parts of the roadmap?
The core technologies required to implement EVM validity proofs for layer 1 are highly shared with the other two areas:
Validity proofs for layer 2 (i.e., "ZK rollups")
"STARK binary hash proofs" stateless approach
Successfully implementing validity proofs for layer 1 can enable extremely lightweight solo staking: even the weakest computers (including phones or smartwatches) would be able to stake. This further increases the value of addressing other limitations of solo staking (such as the minimum of 32 ETH).
Additionally, L1's EVM validity proofs can significantly increase L1's gas limits.
Validity Proof of Consensus
What problem are we trying to solve?
If we want to fully verify Ethereum blocks using SNARKs, then EVM execution is not the only part we need to prove. We also need to prove consensus: the parts of the system that handle deposits, withdrawals, signatures, validator balance updates, and other elements of Ethereum's proof of stake.
This consensus is much simpler than the EVM, but the challenge it faces is that we do not have layer 2 EVM rollups, which is also why most of the work needs to be done anyway. Therefore, any implementation that proves Ethereum consensus needs to be "built from scratch," although the proof system itself can be built on shared work.
What is it and how does it work?
The beacon chain is defined as a state transition function just like the EVM. The state transition function is dominated by three things:
ECADD (for verifying BLS signatures)
Pairing (for verifying BLS signatures)
SHA256 hash (for reading and updating state)
In each block, we need to prove 1-16 BLS12-381 ECADD for each validator (possibly more than one, as signatures can be included in multiple aggregations). This can be compensated for by subset precomputation techniques, so overall, we can say that each validator has one BLS12-381 ECADD. Today, there are about 30,000 validator signatures per slot. In the future, with single slot finality, this could change in either direction (see explanation here): if we take a "brute force" approach, this could increase to 1 million validators per slot. Meanwhile, using Orbit SSF, it will remain at 32,768 or even decrease to 8,192.
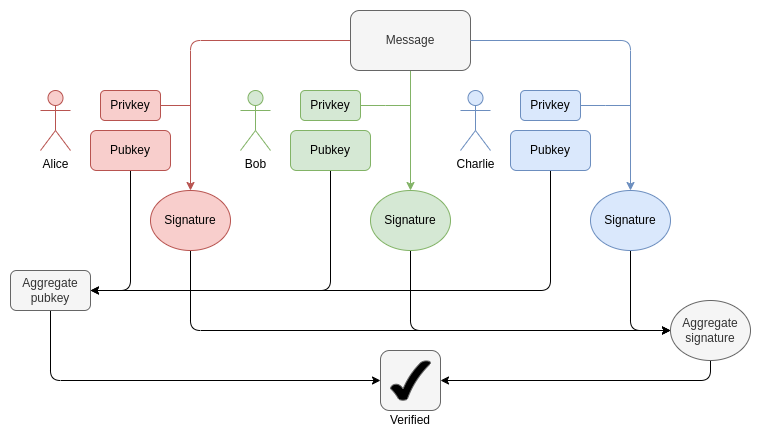
How BLS aggregation works. Verifying aggregated signatures only requires each participant to perform one ECADD instead of ECMUL. But 30,000 ECADDs still require a lot of work to prove.
For pairings, there are currently at most 128 proofs per slot, meaning that 128 pairings need to be verified. With EIP-7549 and further changes, this number may decrease to 16 per slot. The number of pairings is small, but the cost is extremely high: the runtime (or proof time) for each pairing is thousands of times that of ECADD.
A major challenge in proving BLS12-381 operations is the lack of convenient curves where the curve order equals the size of the BLS12-381 field, which adds significant overhead to any proof system. On the other hand, the Verkle tree proposed for Ethereum is built using the Bandersnatch curve, making BLS12-381 itself a natural curve used in SNARK systems to prove Verkle branches. A relatively simple implementation can prove about 100 G1 additions per second; clever techniques like GKR will almost certainly be needed to make the proofs fast enough.
For SHA256 hashes, the worst-case scenario currently is the epoch transition block, where the entire validator short balance tree and a large number of validator balances are updated. The validator short balance tree occupies one byte per validator, resulting in about 1 MB of data being rehashed. This equates to 32,768 SHA256 calls. If the balances of a thousand validators are above or below the threshold needed to update the effective balance in the validator records, this corresponds to a thousand Merkle branches, potentially requiring another ten thousand hashes. The reshuffling mechanism requires 90 bits per validator (thus needing 11 MB of data), but this can be computed at any time during an epoch. In the case of single slot finality, these numbers may increase or decrease again based on details. Reshuffling becomes unnecessary, although Orbit may require some degree of reshuffling again.
Another challenge is the need to read all validator states (including public keys) to verify a block. Reading just the public keys requires 48 million bytes (1 million validators, plus Merkle branches). This necessitates millions of hashes per epoch. If we must prove the validity of proof of stake today, a realistic approach would be some form of incremental verifiable computation: storing a separate data structure within the proof system that is optimized for efficient lookups and proving updates to that structure.
In summary, there are many challenges.
To address these challenges most effectively, a deep redesign of the beacon chain may be required, potentially occurring simultaneously with the switch to single slot finality. This redesign may feature:
Hash function changes: Currently, the "full" SHA256 hash function is used, meaning that due to padding, each call corresponds to two underlying compression function calls. At a minimum, by switching to the SHA256 compression function, we can achieve a 2x gain. If we switch to Poseidon, we could achieve a potential gain of about 100x, which could completely resolve all our issues (at least for hashing): at a rate of 1.7 million hashes per second (54 MB), even a million validator records could be "read into" the proof in a matter of seconds.
If using Orbit, directly store shuffled validator records: If you select a certain number of validators (e.g., 8,192 or 32,768) as the committee for a given slot, placing them directly into adjacent states would require minimal hashing to read all validator public keys into the proof. This would also allow for efficient completion of all balance updates.
Signature aggregation: Any high-performance signature aggregation scheme would actually involve some form of recursive proof, where intermediate proofs of subsets of signatures would be conducted by various nodes in the network. This naturally distributes the proof load across many nodes in the network, significantly reducing the workload of the "final prover."
Other signature schemes: For Lamport+Merkle signatures, we need 256 + 32 hashes to verify a signature; multiplied by 32,768 signers, this results in 9,437,184 hashes. Optimizing the signature scheme can further improve this by a small constant factor. If we use Poseidon, this can be proven within a single slot. However, in practice, using a recursive aggregation scheme can complete this process faster.
What connections exist with current research?
Concise Ethereum consensus proof (only sync committee): https://github.com/succinctlabs/eth-proof-of-consensus
Concise, Helios within SP1: https://github.com/succinctlabs/sp1-helios
Concise BLS12-381 precompiles: https://blog.succinct.xyz/succinctshipsprecompiles/
Halo2-based BLS aggregate signature verification: https://ethresear.ch/t/zkpos-with-halo2-pairing-for-verifying-aggregate-bls-signatures/14671
What remains to be done? What trade-offs are needed?
In reality, it will take us years to prove the validity of Ethereum consensus. This roughly coincides with the time needed to implement single slot finality, Orbit, changes to signature algorithms, and potential security analyses that need to be conducted with sufficient confidence to use "radical" hash functions like Poseidon. Therefore, addressing these other issues is most meaningful, and it is important to keep STARK friendliness in mind while doing this work.
The main trade-off may lie in the order of operations, that is, between a more gradual approach to reforming the Ethereum consensus layer and a more radical "make many changes at once" approach. For the EVM, a gradual approach makes sense as it minimizes the damage to backward compatibility. For the consensus layer, backward compatibility issues are smaller, and it is beneficial to rethink various details of the beacon chain construction more "comprehensively," thereby maximizing SNARK friendliness.
How does it interact with other parts of the roadmap?
In the long-term redesign of Ethereum's proof of stake consensus, STARK friendliness needs to be a primary focus, most notably regarding single slot finality, Orbit, changes to signature schemes, and signature aggregation.
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。




