Article Source: Synced

Theoretical proof! Calibrated language models are bound to hallucinate.

Image Source: Generated by Wujie AI

Although large language models (LLMs) have demonstrated outstanding capabilities in many downstream tasks, there are still some issues in their practical applications. Among them, the "hallucination" problem of LLM is a significant flaw.

Hallucination refers to the generation of seemingly reasonable but false or misleading responses by artificial intelligence algorithms. Since the popularity of LLM, researchers have been working hard to analyze and mitigate the hallucination problem, which makes it difficult for LLM to be widely applied.

Now, a new study has concluded that "calibrated language models are bound to hallucinate." The research paper "Calibrated Language Models Must Hallucinate" was recently published by Adam Tauman Kalai, a senior researcher at Microsoft Research Institute, and Santosh S. Vempala, a professor at the Georgia Institute of Technology. The paper shows that there is an inherent statistical reason for pre-trained language models to hallucinate specific types of facts, which is independent of the Transformer architecture or data quality.

Paper Link: https://arxiv.org/abs/2311.14648

A language model is essentially a probability distribution D on a token sequence (such as words or other character sequences). Each distribution D can be equivalently represented as the log probability on the entire sequence or the conditional log probability of the subsequent token based on the previous token.

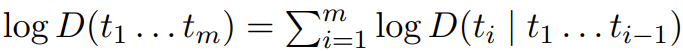
This mathematical equivalence means that any language model can either be used to generate text or predict the next token based on the naturally occurring text.

For example, consider the following sentence:

Alexa Wilkins had a tuna sandwich at Salumeria for lunch last Tuesday because the reviews said that it was divine.

For such a sentence, we can use predictive language models and other techniques to provide recommendations, reducing the number of times one has to click on their phone when inputting. We might hope to have the option of "sandwich" after the word "tuna," as well as other possible words, such as "salad" and "roll." On the other hand, if a generative language model is used to generate randomly, most of these sentences would be incorrect.

This paper demonstrates that a language model with excellent predictive text performance will inevitably produce hallucinations, even under ideal conditions. It is important to note that for common generative language models today, the optimization of predictive text performance is in the "pre-training" phase. In addition, it can provide a lower bound on the hallucination rate; the hallucination rate can reflect the rate at which different types of facts produce hallucinations.

The commonality of the above references and examples is that they are arbitrary, meaning that each item in the 5W (= Who-Ate-What-When-Where-Why simulated facts) cannot be systematically determined by rules—for most of these facts not present in the training data, their truth cannot be determined by people. This is different from facts whose truth can be systematically determined. Even in a simplified environment with several ideal properties, we can quantify the likelihood of language models hallucinating.

Because this paper aims to provide a statistical lower bound, it tends to be simple rather than universal, as the goal of this lower bound is to determine the fundamental reasons for language model hallucinations. Similar to classification tasks (finding the lower bound on the difficulty of classification in a noise-free environment), here we need to find the lower bound on hallucinations that holds even in the simplest setting, which refers to training data being independently and identically distributed and free of factual errors.

Calibrating Generative Models

For a probabilistic predictor, calibration is a natural requirement, as it means that its probabilities can be interpreted as accurate confidence in its own predictions.

Philip Dawid introduced the concept of calibration in 1982, and at that time, he also gave an example that many people are familiar with: when the weather forecast says there is a 30% chance of rain in the next few days, it actually means that it will rain about 30% of the time.

Many researchers have explored calibration metrics for language models. Figure 1 provides an example of multi-class calibration for GPT-4 on a multiple-choice test.

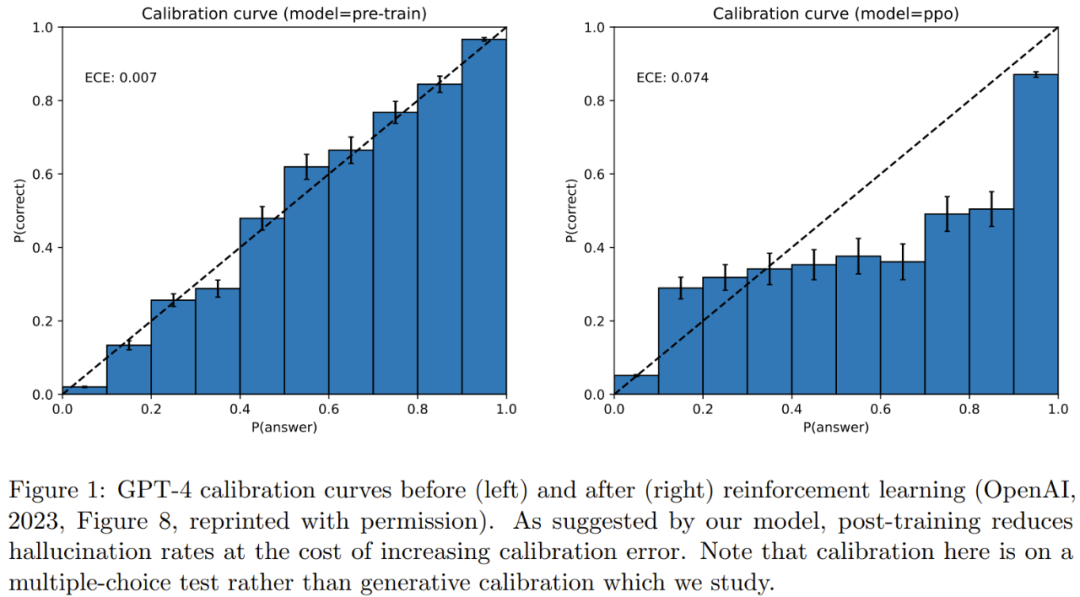
To reduce the problem of hallucination, people often perform alignment operations after training, but research has found that alignment also reduces calibration. Calibration is meaningful (because the probabilities of a calibrated predictor can be interpreted as accurate confidence), and it is statistically achievable. In contrast, not all calibrated models are useful predictors, as a predictor that always outputs the average annual probability of rain can be easily calibrated.

In this article, the researchers provide a natural generalization for the calibration of generative models. Their concept of calibration is different from previous token-level language model calibrations. The problem with analyzing the original token probabilities is that there are many ways to describe any fact in natural language, so the calibrated token probabilities are not very meaningful.

Here's an example to illustrate this. Suppose there is a trigram language model that predicts the probability of the next token based only on the previous two tokens. Trigram models can naturally achieve calibration at the token level, and hallucination is not a major problem for trigram models. This is because they essentially generate meaningless gibberish. In contrast, semantic-level calibration considers the probability distribution based on the information (facts or hallucinations) contained in the text.

How can we determine if a language model has been calibrated? For any probability z ∈ [0, 1], in the information generated by the language model with a probability of about z, such information appears in about z shares of the language naturally expressed (ideally the distribution of the training data).

Reasons for Language Model Hallucination

Hallucination perplexes both language model users and researchers. Researchers have investigated many hypotheses about the reasons for language model hallucinations, from inaccurate or outdated training data to the log-likelihood target for the next token during training.

The reasons for hallucination also include adversarial or out-of-distribution prompts: providing text prefixes that enable the language model to complete existing context. In this new study, researchers found that even with perfect training data and without using prompts, calibrated language models are bound to hallucinate.

Simplified Setting

In the researchers' simplified setting, there is a static language distribution D_L ∈ ∆(X) based on documents (i.e., text strings) x ∈ X and a learning algorithm A.

Learning algorithm A can output a language model, i.e., a distribution D_LM = A (x_train) ∈ ∆(X), based on training data x_train ∈ X^n sampled independently from the static language distribution D_L.

For simplicity, the researchers assume that the training data only contains facts, and each document contains at most one factoid, meaning there are no training hallucinations. The facts here are arbitrary, meaning their truth is usually difficult to determine statistically based on the training set itself; they are not systematic facts (which can be predicted based on the training set by learning the basic rules of correctness), such as 572 120523. There is no statistical reason to suggest that language models would hallucinate on systematic facts.

Furthermore, errors on systematic facts may not be considered hallucinations at all—they are typically classified as reasoning or arithmetic errors.

The researchers assume that each document x ∈ X contains at most one factoid statement f (x) ∈ Y, where a factoid statement refers to arbitrary information that is either true (fact) or false (hallucination), and its truth is difficult to determine statistically based on the training data.

The researchers also adopt another simplification: considering unconditional generation, meaning sampling language models to generate text without using any prompt (equivalent to no string prefix).

Of course, compared to the simplified setting, hallucinations are more likely to occur in more realistic scenarios, where the prompt contains context from a distribution different from the training data.

Results

Assuming n independently and identically distributed samples are sampled from an unknown distribution containing a large number of arbitrary simulated facts, such as 5W samples and indices. The missing mass (in this case, the missing fact p (U)) is the part of the future samples from the fact distribution p that is not observed in the n training samples, where U is a subset of facts not observed in the training data.

The Good-Turing estimate of the missing mass refers to the proportion of samples (in this case, facts) that appear only once in the training data. The researchers refer to this as the MonoFacts estimator:

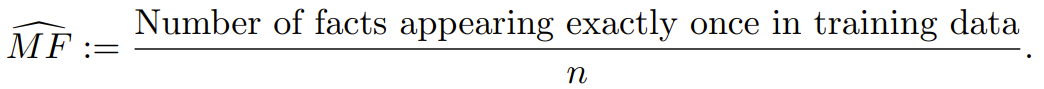
The study shows that for any distribution p, this Good-Turing estimator has a high probability of being within the range of the missing mass:

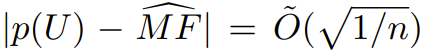
If the correctness of any simulated fact not included in the training cannot be determined, the missing fact rate can provide a lower bound on the hallucination rate. This, in turn, can provide an approximation of:

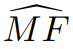
In particular, under the "regularity" assumption of the simulated fact distribution, the simplest boundary (inference 1 in the paper) implies that for any algorithm, there is a ≥ 99% probability on the training set:

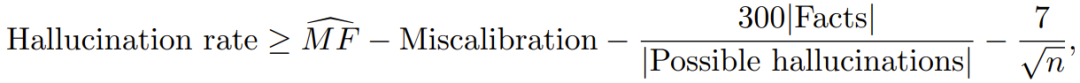
Where the hallucination rate refers to the rate at which the language model produces hallucinations, the next term is the "MonoFacts" estimator for missing facts. The following term quantifies the degree of misalignment between the distribution and calibration. The next term involves the ratio of arbitrary facts to similar information that is incorrect, which is very small for many types of information. The last term is very small because the training set size n for today's language models is very large.

The "regularity" assumption means that, on average, the probability of all unobserved simulated facts being true is equal.

More generally, the probability that this boundary holds is ≥ 1 − δ, where the constant 60 can be replaced by an item that is inversely proportional to δ and proportional to the regularity term on the simulated fact distribution. This regularity term measures the ratio of the most likely simulated facts (unobserved in the training data) to the average unobserved simulated fact probability. For symmetric distributions and other simple distributions, this constant is 1.

To account for bounded regularity, the researchers relaxed it to allow for some negative correlation (e.g., a person cannot have 1000 lunches in 1000 different places on the same day) and to allow for certain simulated facts to have a conditional probability of 0, but it does not allow unobserved simulated facts to have very high probabilities.

Please refer to the original paper for the related proof process.

Explanation

For the above lower bound, the researchers provide the following explanation.

First, a large number of simulated facts should be determined: arbitrary, reasonable, regular simulated facts. They could be articles about 5W and reasonable scientific article citations. Intuitively, there are many more incorrect simulated facts (hallucinations) than facts. Then consider how many of these simulated facts might appear exactly once in the training data. In the case of 5W, it can be imagined that about half of the articles appear exactly once. This indicates that approximately half of the generated results of the calibrated simulated fact model on 5W simulated facts may have hallucination issues.

On the other hand, it can be imagined that the number of articles is much less than n, because the goal of publication is advertising, and each citation may appear multiple times in the training data (i.e., the probability is much greater than 1/n), except for very recent ones (e.g., before other citations appear). This indicates that the missing mass of the articles is very low, and there is no inherent statistical necessity for hallucinations in generating titles of citations.

There are other reasons that may lead to such hallucinations, such as the limited capacity of the model (even though the number of parameters in the language model is much larger than the number of articles, these parameters will inevitably encode many other types of information beyond article titles). This also proves that a reasonable approach to mitigate hallucination problems is to consult a factual database during generation, even if the factual database is entirely based on the training data.

Although there is a tension between factualness and predictive accuracy, the training or "pre-training" objectives of both types of language models are usually to maximize the likelihood on the corpus, which is equivalent to minimizing the "KL divergence," a strong statistical difference indicator between the language model and the distribution of the data it is trained on.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。