Source: Synced

Image Source: Generated by Wujie AI

This year, large language models (LLMs) have become the focus of attention in the field of AI. LLMs have made significant progress in various natural language processing (NLP) tasks, especially in reasoning. However, LLMs still perform poorly in complex reasoning tasks.

So, can LLMs determine if their reasoning is incorrect? A recent study conducted by the University of Cambridge and Google Research found that while LLMs cannot find reasoning errors, they can use the backtracking method proposed in the study to correct errors.

• Paper link: https://arxiv.org/pdf/2311.08516.pdf
• Dataset link: https://github.com/WHGTyen/BIG-Bench-Mistake

This paper has sparked some controversy. Some have raised objections, such as on Hacker News, where some commented that the title of the paper is exaggerated and sensationalized. Others criticized the method proposed in the paper for correcting logical errors, stating that it is based on pattern matching rather than logical methods, which makes it prone to failure.

Huang et al. pointed out in the paper "Large language models cannot self-correct reasoning yet" that self-correction may be effective in improving the style and quality of model outputs, but there is little evidence to suggest that LLMs have the ability to identify and correct their own reasoning and logical errors without external feedback. For example, Reflexion and RCI both use the correction results of basic truth values as a signal to stop the self-correction loop.

The research team from the University of Cambridge and Google Research proposed a new approach: to no longer consider self-correction as a single process, but to divide it into error discovery and output correction processes:

• Error discovery is a fundamental reasoning skill that has been widely studied and applied in philosophy, psychology, and mathematics, giving rise to concepts such as critical thinking, logic, and mathematical fallacies. It is reasonable to assume that the ability to discover errors should also be an important requirement for LLMs. However, the results of this paper indicate that the current best LLMs are still unable to reliably discover errors.
• Output correction involves partially or completely modifying previously generated outputs. Self-correction refers to the correction carried out by the same model that generated the output. Although LLMs do not have the ability to discover errors, this paper shows that if information about errors can be provided (e.g., through a small supervised reward model), LLMs can use the backtracking method to correct outputs.

The main contributions of this paper include:

• Using the prompt design method of thinking chain, any task can be turned into an error discovery task. The researchers collected and released a CoT-style trajectory information dataset called BIG-Bench Mistake, which was generated by PaLM and annotated with the location of the first logical error. The researchers stated that BIG-Bench Mistake is the first dataset of its kind that is not limited to mathematical problems.
• To test the reasoning ability of the current best LLMs, the researchers conducted benchmark evaluations based on the new dataset. The results show that even the current state-of-the-art LLMs find it difficult to discover errors, even in cases of objective and explicit errors. They speculate that the inability of LLMs to discover errors is the main reason why LLMs cannot self-correct reasoning errors, but this requires further research.
• This paper proposes using the backtracking method to correct outputs, using the information about the location of errors to improve performance on the original task. The research shows that this method can correct originally erroneous outputs while minimally affecting originally correct outputs.
• The paper interprets the backtracking method as a form of "language reinforcement learning," which allows for iterative improvement of CoT outputs without any weight updates. The researchers propose using a trained classifier as a reward model for backtracking, and they have demonstrated the effectiveness of backtracking under different reward model accuracies.

BIG-Bench Mistake Dataset

BIG-Bench consists of 2186 sets of CoT-style trajectory information. Each trajectory was generated by PaLM 2-L-Unicorn and annotated with the location of the first logical error. Table 1 shows an example trajectory with an error occurring at the 4th step.

These trajectories come from 5 tasks in the BIG-Bench dataset: word sorting, tracking shuffled objects, logical deduction, multi-step arithmetic, and Dyck language.

They used the CoT prompt design method to invoke PaLM 2 to answer questions for each task. To separate the CoT trajectories into explicit steps, they used the method proposed in the paper "React: Synergizing reasoning and acting in language models," generating each step separately and using a line break as a stop token.

In this dataset, when generating all trajectories, temperature = 0. The correctness of the answers is determined by exact matching.

Benchmark Test Results

Table 4 reports the accuracy of GPT-4-Turbo, GPT-4, and GPT-3.5-Turbo on the new error discovery dataset.

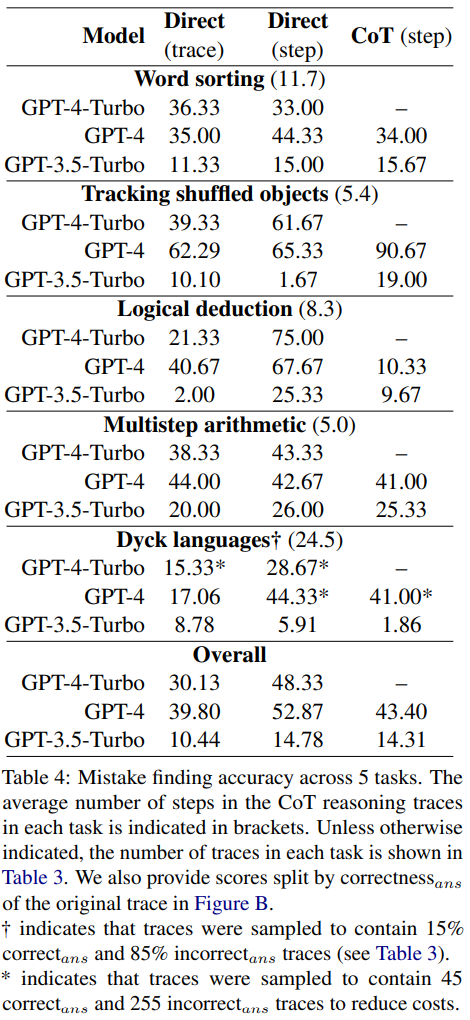
For each question, there are two possibilities for the answer: either there is no error, or there is an error. If there is an error, the number N indicates the step at which the first error occurs.

All models were given the same 3 prompts. They used three different prompt design methods:

• Direct trajectory-level prompt design
• Direct step-level prompt design
• CoT step-level prompt design

Related Discussion

The research results indicate that these three models struggle with this new error discovery dataset. GPT performs the best, but even with direct step-level prompt design, it only achieves an overall accuracy of 52.87.

This suggests that the current best LLMs find it difficult to discover errors, even in the simplest and most explicit cases. In contrast, humans can discover errors without specific expertise and have a high level of consistency.

The researchers speculate that the inability of LLMs to discover errors is the main reason why LLMs cannot self-correct reasoning errors.

Comparison of Prompt Design Methods

Researchers found that from the direct trajectory-level method to the step-level method and then to the CoT method, the accuracy of error-free trajectories significantly decreased. Figure 1 illustrates this trade-off.

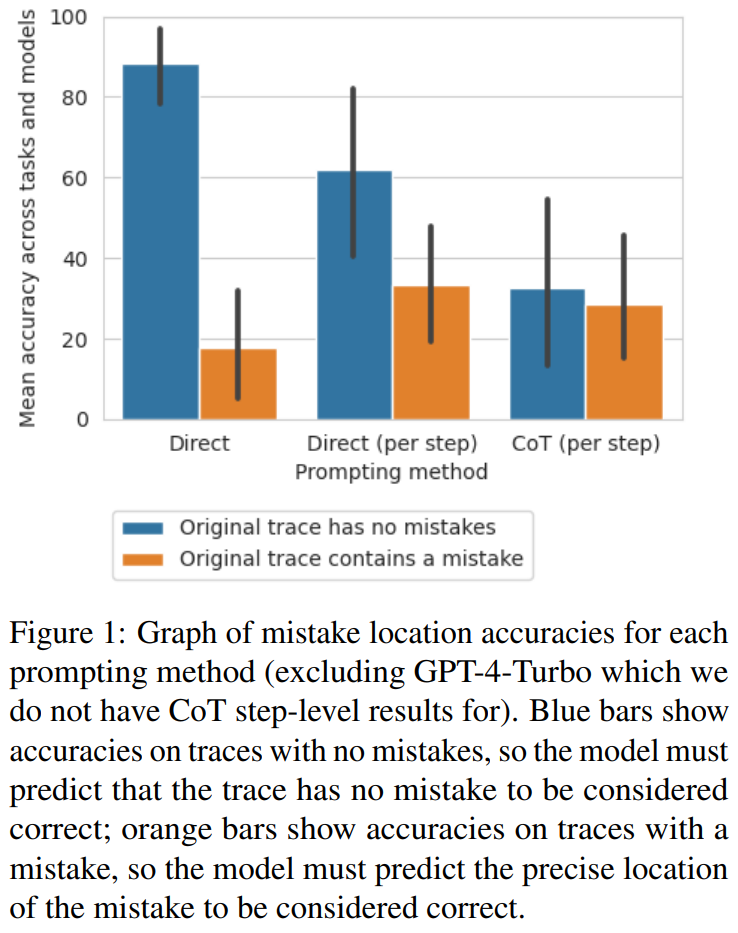
The researchers speculated that the reason for this is the quantity of outputs generated by the model. These three methods involve generating increasingly complex outputs: the direct trajectory-level prompt design method requires a single token, the direct step-level prompt design method requires one token for each step, and the CoT step-level prompt design requires multiple sentences for each step. If there is a certain probability of identifying errors with each generation call, then the more calls there are for each trajectory, the greater the likelihood of the model identifying at least one error.

Using Error Position as a Proxy for Correctness in Few-Shot Prompt Design

The researchers explored whether these prompt design methods could reliably determine the correctness of a trajectory rather than the position of errors.

They calculated the average F1 score based on whether the model could predict the presence of errors in the trajectory. If there is an error, it is assumed that the model predicts the trajectory as "incorrectans." Otherwise, it is assumed that the model predicts the trajectory as "correctans."

Using "correctans" and "incorrectans" as positive labels and weighting based on the frequency of each label, the researchers calculated the average F1 score, as shown in Table 5.

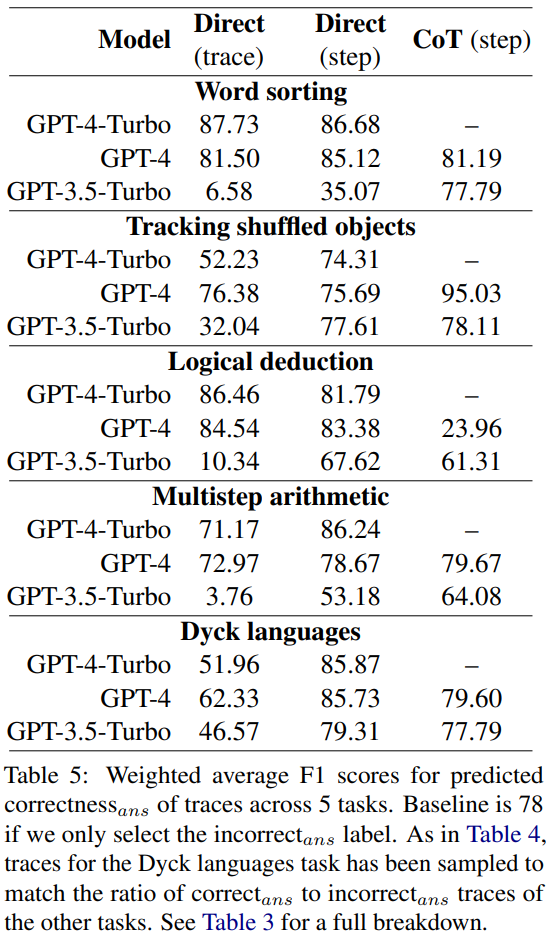
This weighted F1 score suggests that using prompts to find errors is a poor strategy for determining the correctness of final answers.

Backtracking

Huang et al. pointed out that LLMs cannot self-correct logical errors without external feedback. However, in many real-world applications, external feedback is often not available.

In this study, the researchers adopted an alternative approach: using a lightweight classifier trained on a small amount of data as a substitute for external feedback. Similar to a reward model in traditional reinforcement learning, this classifier can detect any logical errors in CoT trajectories and then provide feedback to the generator model to improve the output. If maximum improvement is desired, multiple iterations can be performed.

The researchers proposed a simple backtracking method to improve the model's output based on the location of logical errors:

• The model first generates an initial CoT trajectory. In the experiment, temperature was set to 0.
• Then, the reward model is used to determine the location of errors in the trajectory.
• If there are no errors, the model moves on to the next trajectory. If there are errors, the model is prompted again with the same steps, but this time with temperature set to 1, generating 8 outputs. The same prompt and a partial trajectory containing all steps before the erroneous step are used here.
• Among these 8 outputs, options identical to the previous error are filtered out. The output with the highest log probability from the remaining outputs is selected.
• Finally, the new re-generated steps replace the previous steps, and temperature is reset to 0 to continue generating the remaining steps of the trajectory.

Compared to previous self-correction methods, this backtracking method has several advantages:

• The new backtracking method does not require prior knowledge of the answers. Instead, it relies on information about logical errors (e.g., from the training of the reward model), which can be determined step by step using the reward model. Logical errors may appear in "correctans" trajectories or may not appear in "incorrectans" trajectories.
• The backtracking method does not depend on any specific prompt text or wording, thereby reducing related biases.
• Compared to methods that require regenerating the entire trajectory, the backtracking method reduces computational costs by reusing known logically correct steps.
• The backtracking method can directly improve the quality of intermediate steps, which may be useful for scenarios requiring correct steps (e.g., generating solutions to mathematical problems) and also enhances interpretability.

The researchers experimented with whether the backtracking method could help LLMs correct logical errors based on the BIG-Bench Mistake dataset. The results are shown in Table 6.

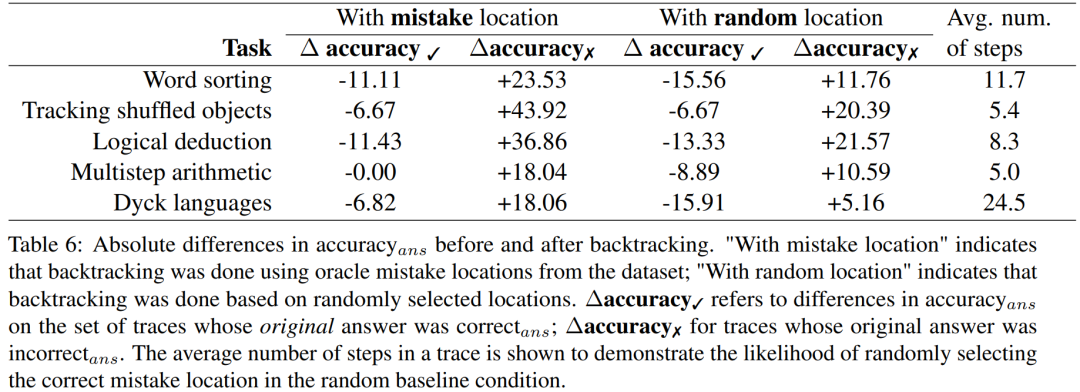
∆accuracy✓ refers to the difference in accuracyans on the trajectory set when the original answer is "correctans."

∆accuracy✗ represents the results for "incorrect_ans" trajectories.

These score results indicate that the benefits of correcting "incorrect_ans" trajectories outweigh the losses caused by changing the originally correct answers. Additionally, while random baselines also saw improvement, their improvement was significantly smaller than the improvement when using the actual error positions. Note that in the random baselines, tasks with fewer steps are more likely to see performance improvements, as they are more likely to find the actual error positions.

To explore which accuracy level of reward model is needed in the absence of good labels, the researchers experimented with using simulated reward models for backtracking; the design goal of this simulated reward model was to produce labels of different accuracy levels. They used accuracy_RM to represent the accuracy of the simulated reward model at specified error positions.

When the accuracy_RM of the reward model is X%, the error positions from BIG-Bench Mistake are used X% of the time. For the remaining (100 - X)%, a random error position is sampled. To simulate the behavior of a typical classifier, error positions are sampled in a way that matches the dataset distribution, and care is taken to ensure that the sampled error positions do not match the correct positions. The results are shown in Figure 2.

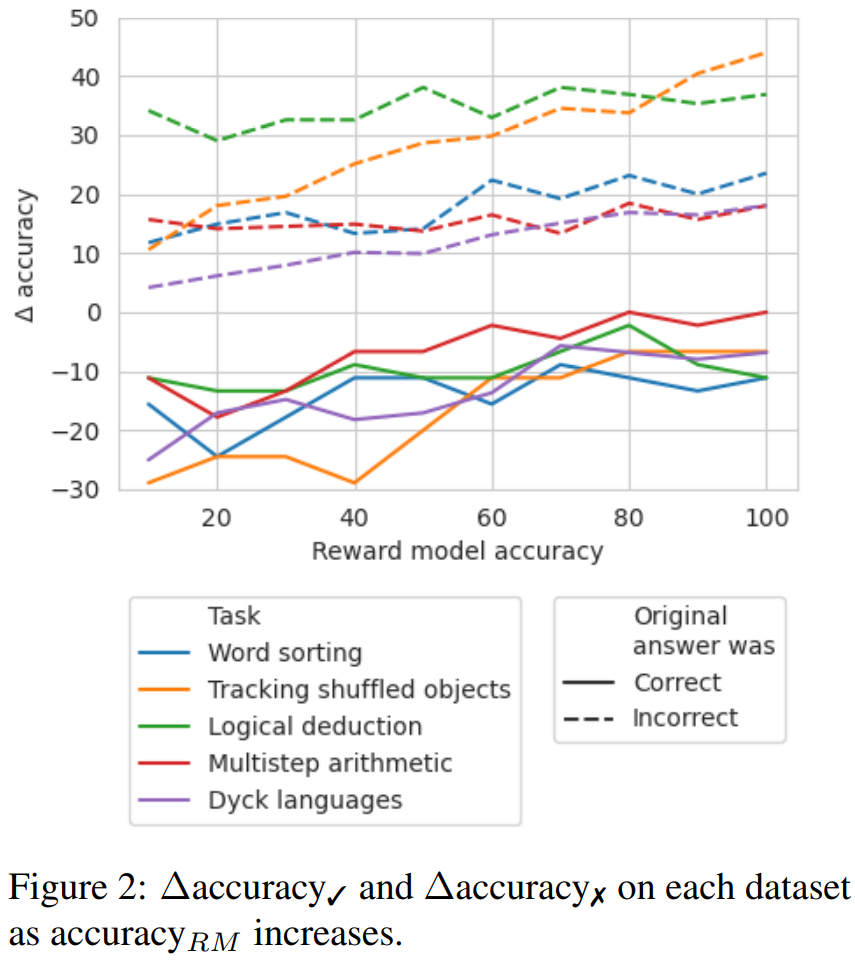
It can be seen that the loss in ∆accuracy✓ begins to stabilize at 65%. In fact, for most tasks, at an accuracy_RM of approximately 60-70%, ∆accuracy✓ is already greater than ∆accuracy✗. This indicates that even without golden standard error position labels, backtracking remains effective, although higher accuracy leads to better results.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。