In the next few years, the number of proofs generated per second will more than double, and then gradually approach the gains of underlying general-purpose computing.
Written by: STANFORD BLOCKCHAIN CLUB, ROY LU
Translated by: DeepFlow Tech
Note: This article is from the Stanford Blockchain Review, and DeepFlow Tech is a partner of the Stanford Blockchain Review, exclusively authorized for translation and reprint.

Introduction
In this article, we will explore how zero-knowledge proofs are changing our lives beyond Web3. I will discuss the leverage effect of performance improvement, propose the "Moore's Law of Zero-Knowledge," and identify patterns of value accumulation.
Zero-knowledge is one of the most revolutionary technologies in today's Web3, with enormous potential in scalability, identity verification, privacy, and more. However, its current performance limitations restrict its potential in many potential applications. Nevertheless, as ZK technology continues to mature, I believe that ZK technology will experience exponential growth and be widely applied in Web3 and traditional industries. Just as Moore's Law predicts a doubling of chip transistor density every two years, I am now proposing a similar exponential law for zero-knowledge proofs, specifically:
In the next few years, the number of proofs generated per second will more than double, and then gradually approach the gains of underlying general-purpose computing.
Overview of Moore's Law
Moore's Law, proposed by Gordon Moore, co-founder of Intel in 1965, predicts that "the complexity of semiconductor electronic integrated circuits will double every two years." Over the past 58 years, Moore's Law has driven almost every aspect of mobile computing, machine learning, and our digital lives, thereby changing the way we interact with technology.
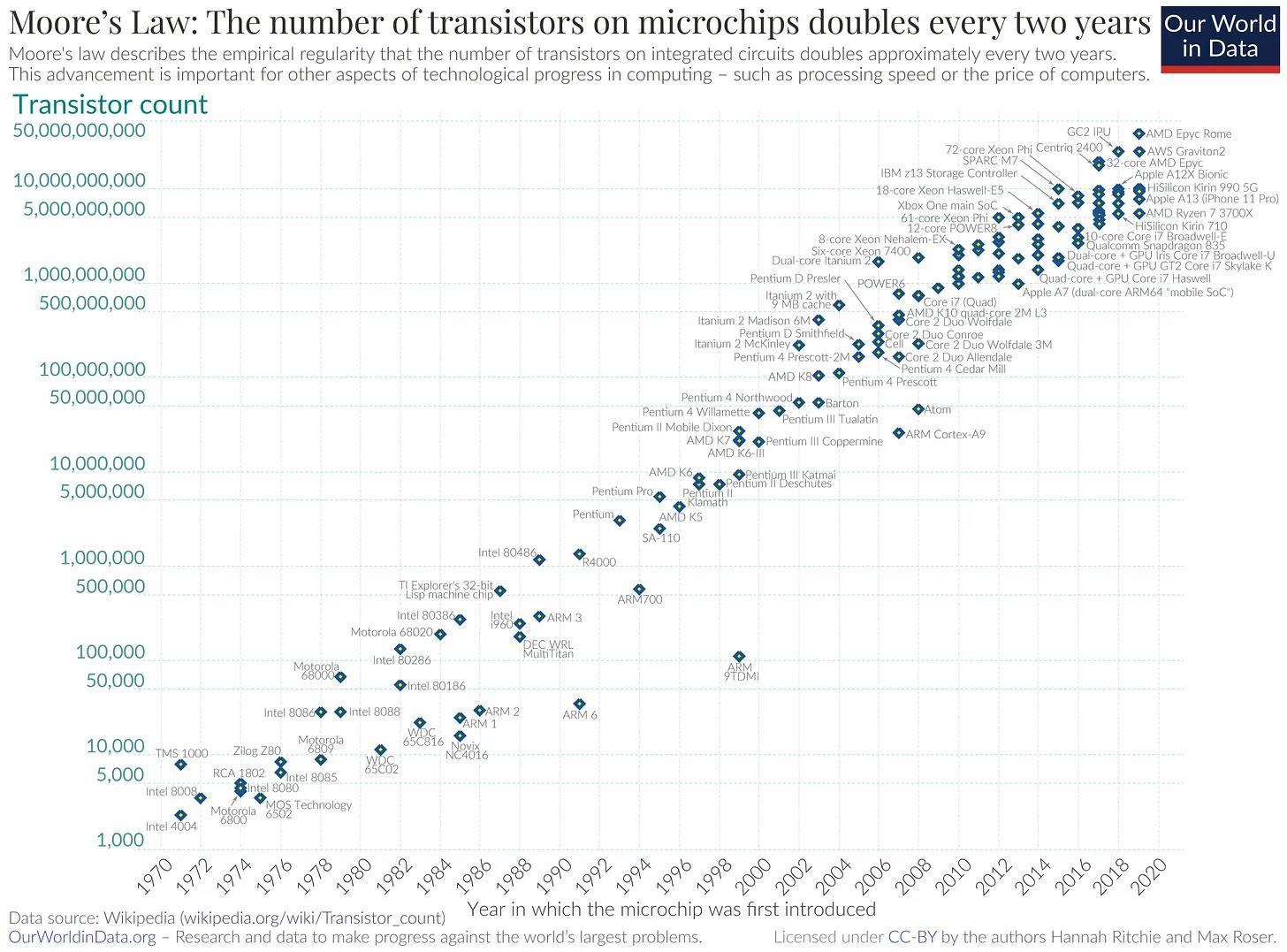
Gordon Moore empirically observed that as the number of transistors on a chip doubled, manufacturing costs remained essentially constant due to economies of scale. He further noted that the demand for computing power would drive investment in increasing transistor density.
As computing power exponentially increased on ever smaller chips, this magnitude of change in the number of transistors transformed the quality of our interactions with and use of computers.
Our smartphones are more powerful computers than the Apollo 11, conveniently fitting in our pockets, enabling us to stream content from any website and communicate with anyone anywhere in the world. The training of large language models paved the way for the release of ChatGPT, transforming the way we interact with information from data retrieval to intelligent synthesis.
The Emergence of Zero-Knowledge Proofs and Web3
Just as the exponential growth of transistors in general computing has led to a qualitative change in the way we interact with modern technology, the exponential growth of zero-knowledge proofs will usher in a new wave of application layer experiences. Fundamentally, zero-knowledge proofs endow privacy, correctness, and scalability, rooted in the privacy of zero-knowledge, provable correctness, and recursive succinctness. These characteristics represent a fundamental shift towards a new computing paradigm.
Private Computation
Zero-knowledge allows computation to be performed in private modules, with only the shared and externally verified results. In a real-world example, if a bank adopts zero-knowledge computation, it can prevent identity theft. For instance, users can allow the loan approval process to run on their identity information and credit history to obtain loan approval without revealing their sensitive data to the bank—privacy is protected. In Web3, ZK powers fully private L1 networks (such as Aleo and Mina) or private payment networks (such as Zcash, zk.money, Elusiv, and Nocturne). ZKP also allows teams like Renegade to run dark pools to list trade orders without affecting market prices. Value is transmitted without revealing users' private data.
Provable Correctness
For opaque computations, zero-knowledge provides traceability of inputs, outputs, and processing. An example is decentralized machine learning, democratizing artificial intelligence through a network of remote computing nodes. ZKP can prove the data, weights, and training rounds in machine learning, establishing correctness as expected. In Web3, teams like Gensyn and Modulus Labs have begun implementing zkML, while general ZKVMs like Risc Zero are also in implementation. ZKP is used in ZK bridges such as Polymer, Succinct Labs, Herodotus, and Lagrange to prove the correctness of cross-chain states. ZK also enables applications like Proven to prove the correctness of reserves.
Recursive Succinctness
ZK can also fold a stack of proofs into a single proof. Another real-world example is authenticity tracking in the supply chain. Manufacturers at each step of the supply chain can use ZKP to prove the authenticity of their products without revealing sensitive manufacturing information. These ZKPs are then recursively proven to generate a final ZKP, proving the correctness of the entire supply chain—achieving scalability. In Web3, thousands of transaction ZKPs can be merged into a single proof, powering L2 networks like Starkware, Scroll, and zkSync, significantly increasing blockchain throughput.
Defining Moore's Law of Zero-Knowledge
From the above, we have seen the abstract similarities between transistors driving application layer breakthroughs and ZKP unlocking a similar wave of innovation in Web3. Now is the time to derive a specific definition of "Moore's Law of Zero-Knowledge" by comparing general computing and zero-knowledge computing.
General Computing and Zero-Knowledge Computing
In general computing, gates are composed of metal-oxide-semiconductor transistors. Each gate can belong to one of multiple operations such as AND, OR, XOR, etc. These operations collectively make programs run.
Under similar conditions, zero-knowledge computing is more expensive than general computing. For example, "using Groth16 for a 10kb SHA2 hash takes 140 seconds, while without zero-knowledge, it only takes a few milliseconds." This is because ZK computation involves complex arithmetic operations for each operand.
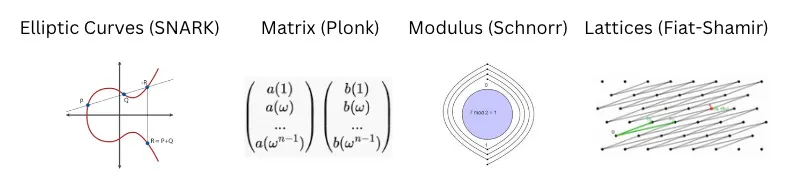
In zero-knowledge computing, operands can be represented in a finite field. In the case of SNARKs, each operand is processed on an elliptic curve. In other variants of zero-knowledge, operands may be composed of matrices, lattices, or arrays, which are also complex mathematical structures for arithmetic operations. Performing simple addition, subtraction, and multiplication with these operands is very expensive. Data input is transformed into a finite field, rather than numbers. The complexity of these structures forms the basis for the security of encryption technology. While the arithmetic details are beyond the scope of this article, the key point is that, just as logic gates execute in physical circuits, zero-knowledge logic executes in software circuits.
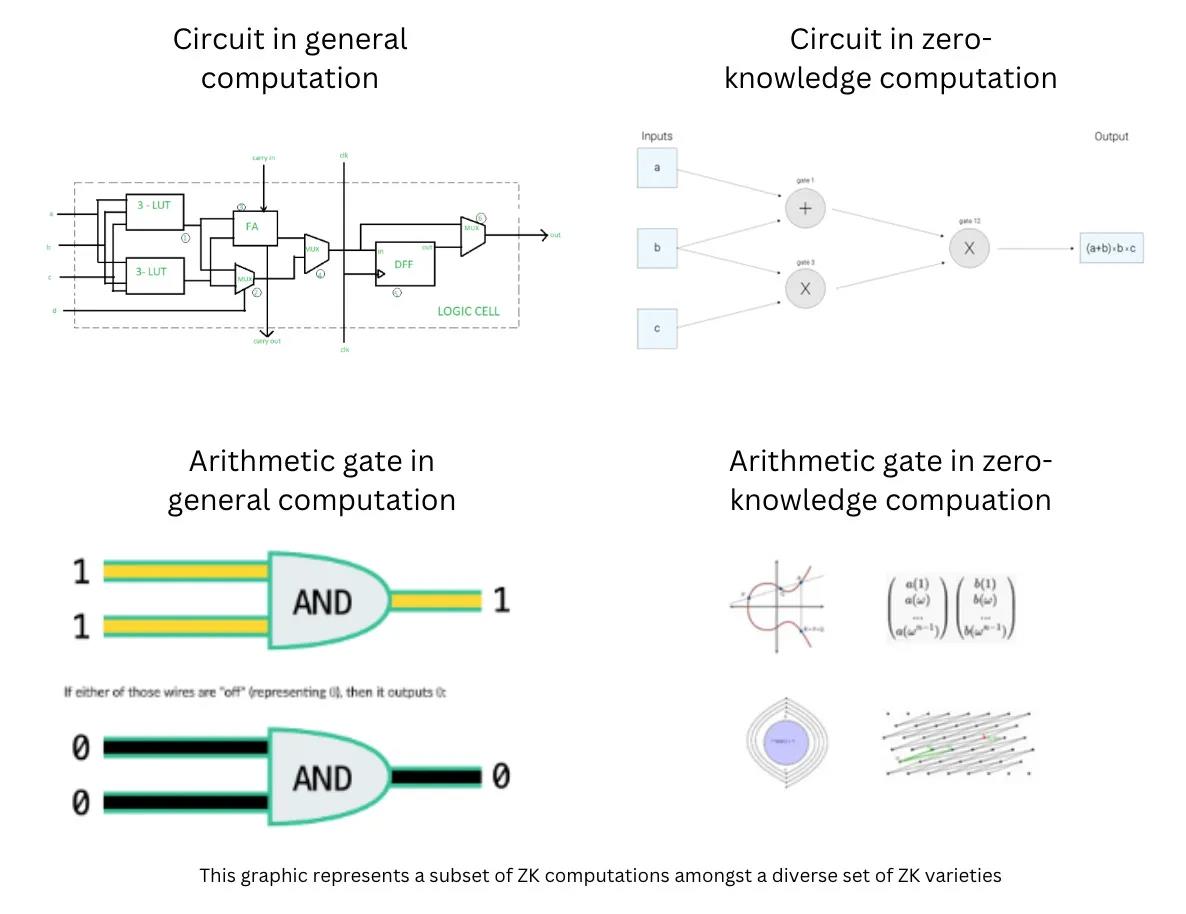
Therefore, in general computing, performance improvements are governed by physical laws, while in zero-knowledge computing, performance improvements are governed by mathematical laws. Thus, we recognize that while hardware acceleration also brings significant gains, applying Moore's Law to zero-knowledge exists in the software domain, not necessarily the hardware domain. Based on these fundamental principles, we can also derive the specific form of Moore's Law in zero-knowledge.
Discontinuous Breakthroughs in Zero-Knowledge
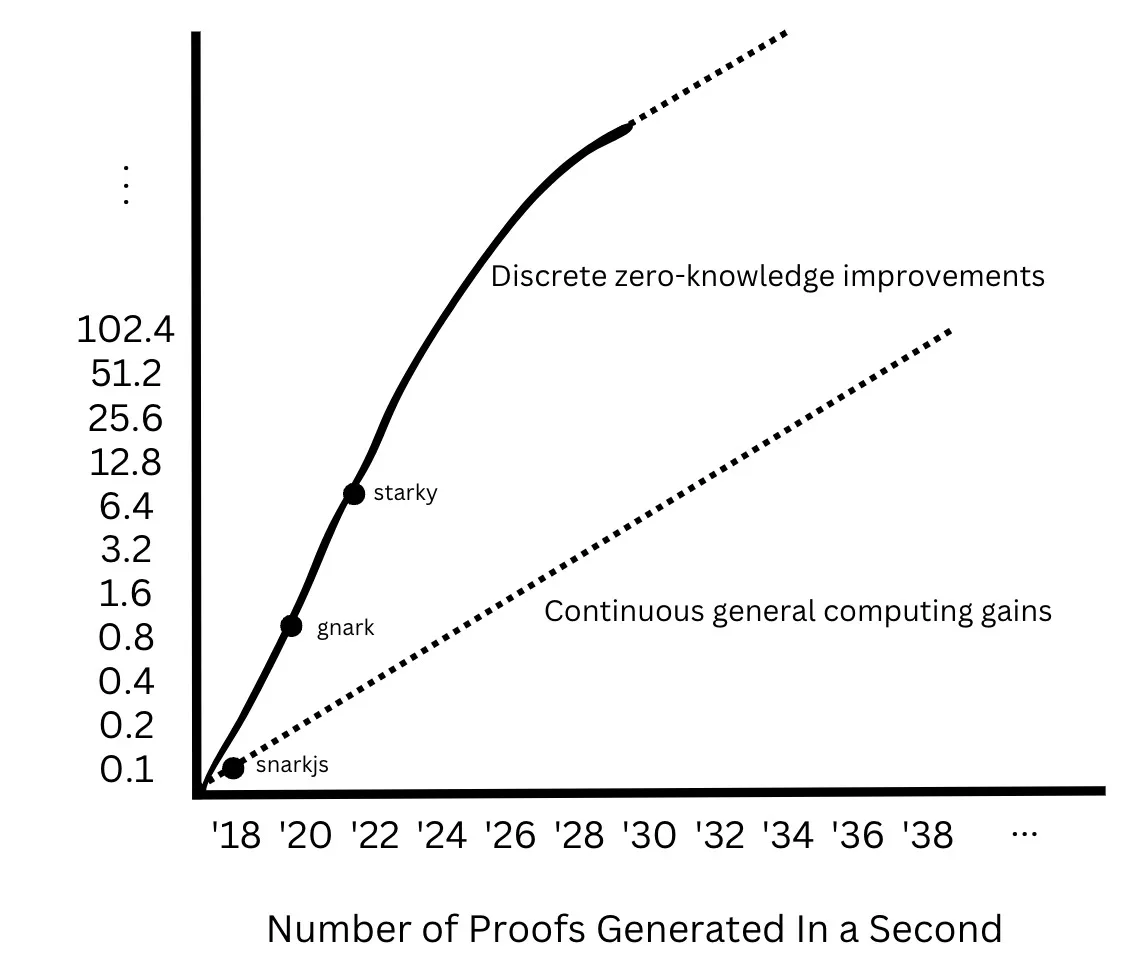
Perhaps the most important observation is that we find that while improvements in general computing are continuous, improvements in zero-knowledge computing are incremental.
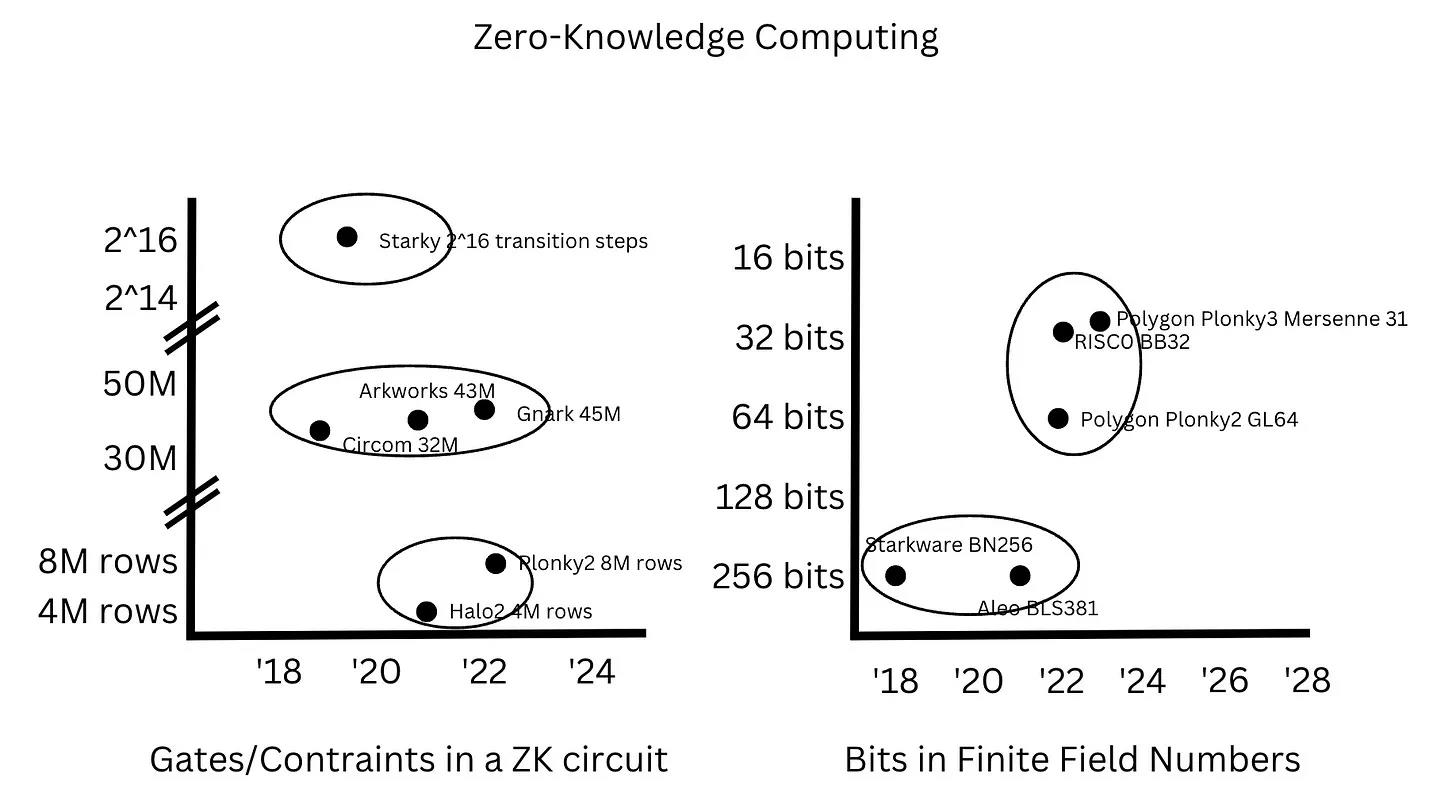
Specifically, from 2005 to 2020, the number of CPU cores roughly doubled every five years, and clock frequencies roughly doubled from the 1990s to the 2010s. On the other hand, the number of constraints in ZK circuits did not "improve" continuously, but jumped from 30-40M constraints in SNARKs to 4-8M in PLONKs, and then jumped to 2^14-2^16 transformation steps in STARKs. Similarly, the number of bits in finite field numbers was approximately 256 bits from 2018 to 2022, then jumped to 32 bits between 2022 and 2023 to take advantage of 32-bit registers.
Furthermore, the latest developments in HyperSpartan support a customizable constraint system (CCS) that can capture R1CS, Plonkish, and AIR simultaneously without additional overhead. The introduction of SuperNova is built on top of Nova, a high-speed recursive proof system with a folding scheme compatible with different instruction sets and constraint systems. These two advances further broaden the design space of ZK architecture.
Based on these findings, the fundamental Moore's Law in zero-knowledge is not based on any single continuous improvement vector, but on the overall performance gains of the number of proofs generated within a given time, driven by discontinuous improvements. I believe that before inheriting the gains of underlying general-purpose computing, Moore's Law in zero-knowledge will undergo discrete revolutionary leaps:
In the next few years, the number of proofs generated per second will more than double, and then gradually approach the gains of underlying general-purpose computing.
Reducing the Cost of Zero-Knowledge Proofs
As mentioned earlier, the current stage of zero-knowledge proofs is too fragile and expensive for widespread potential applications. In particular, the cost of verification far exceeds the cost of proof generation. Based on rough estimates, the cost of generating zero-knowledge proofs is less than $1, based on the following facts: 1) on Amazon AWS, the cost of an EC2 instance with 16 CPUs and 32GB of memory is $0.4 per hour, and the cost of decentralized computing nodes is expected to be lower; 2) Polygon Hermez costs $4-6 per hour, generating approximately 20 proofs per hour.
However, the on-chain cost of verification is still high, with each verification consuming 230,000 to 5,000,000 gas, roughly equivalent to $100-2000 per verification. Although ZK Rollups benefit from economies of scale by spreading the cost across thousands of transactions, other types of ZK applications must find ways to reduce verification costs in order to achieve the aforementioned application layer innovations, thereby improving the quality of life for end users.
Given that breakthroughs in zero-knowledge proof capacity may occur in discontinuous and discrete steps, let's take a look at potential areas where these breakthroughs might occur. Here are some potential optimization methods listed in zkprize:
Algorithm optimization, including multiple scalar multiplication (MSM) and number theoretic transform (NTT), which are often used to accelerate elliptic curve cryptography and can themselves be hardware accelerated. The Fourier transform is an example of NTT that has been optimized in various implementations.
Parallel processing can increase the throughput of zero-knowledge by delegating parts of data structure preprocessing, circuit evaluation, or proof generation to multiple processing units or threads.
Compiler optimization can improve register allocation, loop optimization, memory optimization, and instruction scheduling.
In terms of algorithm optimization, an example is the arithmeticization from R1CS in SNARKS to Plonkish in Halo2, Plonky2, and HyperPlonk, which are different from the AIR used in Starky proofs. Additionally, the latest developments in folding schemes are exciting, as HyperNova can support incremental verifiable computation with a customizable constraint system. In parallel processing, the Polygon team's release of Plonky2 recursion expands the possibilities of parallel proof generation. In terms of compiler optimization, the use of LLVM for zero-knowledge is very interesting, as the intermediate representation (IR) can be compiled into opcode agnostic of the instruction set. For example, Nil Foundation's ZK-LLVM and Risc0's zkVM also use LLVM to generate zero-knowledge proofs that trace the execution of each step. A general-purpose ZKVM or LLVM extends zero-knowledge to use cases beyond blockchain and increases the portability of code for a wider range of developers.
Impact on Zero-Knowledge Builders
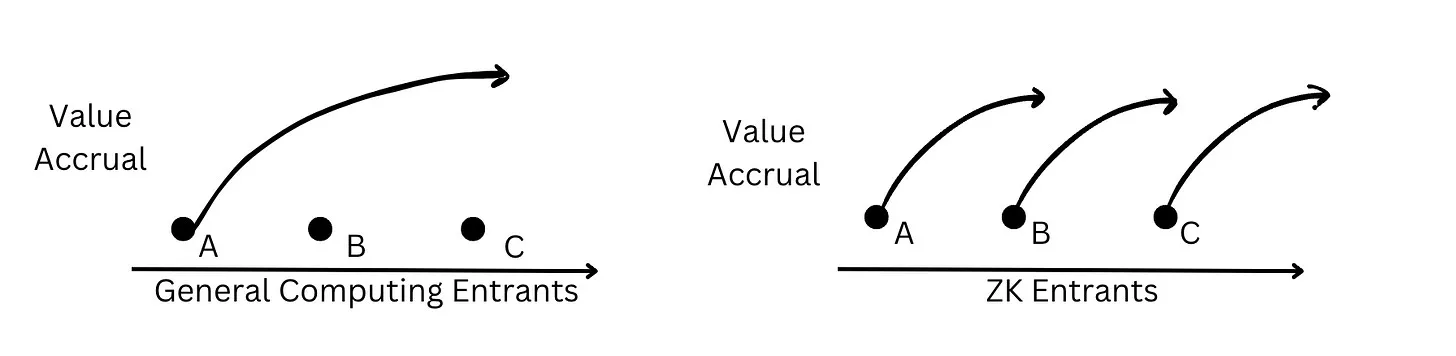
In general computing, value accumulation typically benefits existing participants; for example, chip manufacturers benefit from moats formed around capital investments that support incremental improvements in manufacturing technology to produce increasingly smaller chips. However, since innovation in zero-knowledge occurs through discrete revolutionary leaps, new teams still have ample opportunities to break through with research-driven technical capabilities, such as inventing new proof systems, surpassing existing participants.
Based on this theory, there are several key points for zero-knowledge builders in Web3:
Zero-knowledge builders should consider modular design. Protocol builders involving zk circuits should consider modular design, allowing them to replace components with the most advanced ZK technology.
Participants can benefit from research-driven disruption. For teams with research capabilities, it is possible to propose or pioneer revolutionary new proof systems and surpass existing teams.
Vertical integrators can benefit from a combination of the latest technologies. As every layer of the zero-knowledge stack, from hardware to compiler to circuit, can undergo its own improvements, vertical integrators can modularly adopt the latest technologies and provide state-of-the-art ZK technology to application teams at the lowest cost.
Based on these points, I anticipate three major developments in the industry:
New teams surpassing current ZK protocols through technical breakthroughs.
Existing protocols seeking moats based on ecosystems rather than technology.
Vertical integrated ZK providers emerging to provide the latest technology at lower costs. Innovation and disruption will occur in this rapidly evolving field.
Conclusion
The paradox in technology is that when technology is done well, it becomes invisible. We don't think about the cup when we drink water, just as we don't notice the computer chip when we send an email. When technology is done well, we don't notice the existence of proofs, but we find our transactions more private, information more accurate, and Rollups faster and cheaper. Therefore, zero-knowledge proofs may eventually become integrated into the foundation of our lives, just as transistors, microchips, and now artificial intelligence have become integrated into our daily lives.
We don't need to think about how zero-knowledge prevents fraud in elections, saves transaction costs by disintermediating from the financial system, or democratizes AI training through decentralized computing using ZK. Perhaps one day, just as we consider Moore's observation "the number of transistors on a circuit board will double every 18-24 months" as the so-called "law," we will also consider "the number of zero-knowledge proofs per second will grow exponentially every year" as a matter of course, while enjoying the fruits of these innovations. When goals are achieved more simply, no one will keep praising zero-knowledge, and we will continue to live our daily lives.
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。




