In June 2025, Bitcoin core developers merged a pull request that essentially removed the OP_Return size limit policy in the software. We have previously expressed our views on this topic, arguing that in the long run, the fee market is our tool to combat spam transactions, rather than policy restrictions and filters.
However, the decision to remove the OP_Return size limit sparked controversy in certain Bitcoin community groups, with some claiming it would encourage spam transactions, such as on-chain JPG images. Another complaint was that core developers did not take sufficient action to combat spam transactions and did not prevent JPG images on the blockchain. When Udi Wertheimer mocked anti-spam advocates by embedding images into the blockchain through "Taproot Wizards," those opposing spam transactions or supporting filters hoped or expected Bitcoin core developers to take action to stop it, but they did not.
As a result, more and more people began running Bitcoin Knots, a client that is said to be more effective at combating spam transactions through filters. According to Coin.Dance data, as of August 25, 2025, about 17% of connectable nodes were running Bitcoin Knots.
Information Theory
While some criticize Bitcoin core developers for not combating images, others respond that core developers should not play a "whack-a-mole" game, as it would only waste time.
This essentially means that Bitcoin core could take measures to combat images, but it would only be temporarily effective, as spam transaction senders will always find ways to bypass defenses. It is an asymmetric battle; for every step spam transaction senders take, the effort they expend is far less than that of those trying to stop spam transactions. This war will eventually come to an end, and spam transaction senders will ultimately prevail.
Why should Bitcoin core developers be obligated to invest time and energy into a battle they will ultimately lose? Therefore, it is understandable that many developers are reluctant to engage in this fight.
From the perspective of those supporting filters, they may also acknowledge this point, but they argue that the existence of filters is to increase the cost of spam transactions, even if it is possible to bypass them with enough effort.

Claude Elwood Shannon
When it comes to using filters to block spam information, one might think this is a doomed battle, as it relates to "Information Theory." Information theory is a science formally proposed by Claude Shannon in the 1940s that studies the communication of information. Shannon introduced some core concepts of computer science and information transmission.
Therefore, simply using "Information Theory" to conclude that supporters of filtering are completely wrong may be somewhat inappropriate. A more accurate statement is that information theory can be seen as a scientific field where people can argue that images can always be stored in seemingly random data, which is necessary for Bitcoin transactions. Thus, saying that "Information Theory" proves something may not be fair.
Necessary Data for Transactions
At the most basic level, Bitcoin financial transactions have some necessary components to ensure that transactions function properly. Specifically, each transaction requires a public key and a signature. Without these two core components, Bitcoin transactions cannot operate. Therefore, these components must be on-chain.
When receiving Bitcoin, a Bitcoin address must be provided. Since these addresses are generated through hash functions, the addresses themselves cannot be distinguished from random data. Therefore, data related to images can be used as "fake addresses," and Bitcoin can be sent to these addresses.
These fake addresses will enter the public blockchain in the form of output hashes. Since there are no public keys associated with these addresses, the Bitcoin sent to them will never be recoverable.
Understanding this as "Information Theory" means that the hash function is a random process that produces entropy that can be used to transmit information. No filter can truly stop this. These fake addresses have been used in Bitcoin's history, and here are some examples.
Fake Addresses
In December 2013, someone encoded an image of former South African President Nelson Mandela into the Bitcoin blockchain using a "fake address." The image is shown below.

Sources: https://mempool.space/tx/78f0e6de0ce007f4dd4a09085e649d7e354f70bc7da06d697b167f353f115b8e, https://mempool.space/tx/8881a937a437ff6ce83be3a89d77ea88ee12315f37f7ef0dd3742c30eef92dba,
List of associated fake addresses: https://bitfossil.com/78f0e6de0ce007f4dd4a09085e649d7e354f70bc7da06d697b167f353f115b8e/ADD
Long before this, in May 2011, fake and unspendable addresses were used to store the Bitcoin logo in the Bitcoin blockchain.

Source: https://mempool.space/tx/ceb1a7fb57ef8b75ac59b56dd859d5cb3ab5c31168aa55eb3819cd5ddbd3d806
It should be noted that using fake addresses in this way for spam transactions does indeed make running nodes more difficult, as it may cause the UTXO set to expand. This is also part of the reason for allowing OP_Returns.
Prohibiting Fake Addresses
If someone wants to stop fake addresses, it is theoretically possible. However, this would require a fundamental restructuring of Bitcoin and protocol changes. One way to prevent such addresses could be to require transaction outputs to include a digital signature, thereby proving the existence of a public-private key pair and that the address is "real." Thus, both transaction inputs and outputs would need a signature.
While this is theoretically feasible, it would be a massive undertaking and would come with the following drawbacks:
All existing wallets would be incompatible with the new transaction format, and old transactions would be disabled. There has never been a case of disabling old transactions, which would threaten monetary sovereignty, and people could lose funds as a result.
The transaction process would need to change, requiring the receiver not only to provide an address to the sender but also a digital signature.
The number of on-chain signatures would increase, making transaction sizes larger and harming Bitcoin's scalability.
This could encourage address reuse, harming privacy.
This would be a protocol change requiring broad consensus, potentially necessitating a hard fork.
Many features of Bitcoin, such as P2SH or Taproot, might need to be removed, or at least we would not be able to enjoy the benefits of P2SH.
More public keys would be visible, making Bitcoin more susceptible to quantum attacks.
As you can see, the above approach is completely impractical and would lead to utter disaster. However, even such an extreme change might not stop JPG images. After carefully ruling out all other options, people could still store images in private keys, as private keys are just random data, which are a necessary component of Bitcoin. Therefore, for Bitcoin developers, this remains a battle they will lose. They would invest tremendous effort into completely restructuring Bitcoin and all wallets, while spam transaction senders would simply and relatively easily turn to other methods.
JPG Images as Private Keys
A Bitcoin private key is simply a 256-bit random number. Such a number is mathematically equivalent to a 16x16 pixel image, where each pixel is either black or white. All private keys can be represented by these tiny images.
We created a Bitcoin private key by generating a portrait image like the one below. We saved this image in JPG format, as shown below.
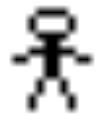
From the perspective of those supporting filters, although generating a private key through image creation may not be the safest way to use Bitcoin, this behavior could still be considered illegal. It is viewed as spam information because, from certain angles, we are placing JPG images onto the blockchain or using JPG images within the blockchain.
However, of course, using filters to restrict this use of Bitcoin is mathematically impossible, as these images are mathematically equivalent to any other means of expressing a private key.
To generate a private key from an image, each pixel can be assigned a value of 1 or 0 based on its black or white attribute, as illustrated by the following 256-bit number.

A Bitcoin address generated from the above private key is as follows:
1JfvNAje3G3Gvt41hL4P7Eh96NLj79o5v7
This is just using a private key to generate a small image. But of course, this can be scaled up. You can generate a 1MB large image and then break it down into thousands of private keys. These private keys can be used for transactions and to launch spam attacks on the blockchain. Such behavior is likely to be considered spam. However, generating an image with a single private key and using it to process "financial transactions," even the most extreme supporters of filtering may not view it as spam, despite it involving images.
Vulnerable Signatures
The method of putting "images" on-chain described above is not particularly effective. First, when conducting Bitcoin transactions, the private key should be kept secret, while spam senders want the image to be publicly visible.
However, an insecure signature can be generated such that the private key can be calculated from the on-chain data. If the image data can be determined from the available data on the blockchain, it is equivalent to putting the image on the blockchain.
To sign a message with ECDSA, various calculations are required during the signature generation process. One of these calculations requires a randomly generated value K. Bitcoin has historically faced various security issues due to poor randomness in the use of K values, such as the issue with the Blockchain.info wallet in August 2013. Due to a security vulnerability, the same K value was used to sign multiple transactions, leading to the theft of user funds.
Another example of using the same K value across different messages is Sony's Playstation 3 console, which used the same K value for each game. This vulnerability was disclosed at the 2010 Chaos Communication Congress in Germany. Days later, the legendary hacker George Hotz published the private key for the Playstation 3. Therefore, K values must be kept secret and different K values must be used for each message; otherwise, anyone can calculate the private key.
We developed a basic scheme using these vulnerable K values to embed a JPG image into our private key, allowing anyone with access to the blockchain to calculate these private keys. We then broadcast our transaction, using this system to place a JPG image on the blockchain. We believe this is the first significant/meaningful image stored in vulnerable private keys in Bitcoin's history.
In a single input single output transaction, we created a 15-of-15 P2SH multi-signature input. The total size of the transaction was 1,690 bytes. Since the input is a 15-of-15 multi-signature input, there are a total of 15 signatures and 15 public keys on-chain. Among the 15 associated private keys, 14 are JPG images, which is the image at the top of this article. To pay homage to the 2011 image, it features a black and white Bitcoin logo.

Source:
https://mempool.space/tx/700f1b8216d4b28cdbf7fe8abb4061763d51019b2a1007a3d811f50e320db98a
In our structure, to create vulnerable signatures, we did not use the same K value for multiple messages. We chose a system with the following rules:
The first K value is the SHA256 hash of the first public key
The second K value is the SHA256 hash of the first K value
The third K value is the SHA256 hash of the second K value
And so on…
The 15th K value is a truly securely generated random number
Thus, to an ordinary observer on the blockchain, the signatures appear quite secure. However, once someone knows how we chose the K values and what they are, they can calculate the 14 private keys. We can continuously change this scheme; if the filtering supporters try to stop us by filtering exposed K values, we can develop a new, more secure scheme, always staying one step ahead.
Since all 15 private keys are needed to spend the funds at that address, and only 14 private keys are vulnerable, the funds remain secure, and attackers cannot steal the funds before the transaction is confirmed. Therefore, we achieved the goal of securing the funds while allowing the private keys represented as images to enter the public domain.
According to the formula from Wikipedia, the formula for calculating the private key is as follows:
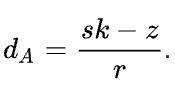
It is worth noting that the S and R values are available in the signature, while Z is the message hash. Therefore, if someone knows the K value, they can easily calculate the private key.
We used the following Python script to perform the calculations. The script below calculates the first private key.
from hashlib import sha256 # transaction id: 700f1b8216d4b28cdbf7fe8abb4061763d51019b2a1007a3d811f50e320db98a
# compute the first k using the first public key (onchain data)
k_hex = sha256(bytes.fromhex('028f98d43a28e131ec1ca2bed82007e36b811a703046213390b308823cea98774a')).digest()
k_list = [int.from_bytes(k_hex, 'big')]
# compute the subsequent k
for i in range(13):
k_hex = sha256(k_hex).digest()
k_list.append(int.from_bytes(k_hex, 'big'))
# r and s of the first signature (onchain data)
r = 0x468ee7af91e05978ca8c1683f6191776553d23eaa1121007d27e52c53ad1d864
s = 0x5fd79b53024ce968dea52744542b0671a7a35b17b72b7d46a4c54e9709ae2a45
# the first k value
k = k_list[0]
# z is the SignatureHash
z = 0x1cd9060f9b6caf7b05804999133f2d979c62899ac0c0c2c6e5f943fd1d83f910
# ORDER is a constant # [https://github.com/bitcoin/bitcoin/blob/master/test/functional/test_framework/crypto/secp256k1.py#L167](https://github.com/bitcoin/bitcoin/blob/master/test/functional/test_framework/crypto/secp256k1.py#L167)
ORDER = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
# There are two potential private keys for each signature, but only one is correct.
# In this scenario, the correct key is private_key_2.
private_key_1 = ((s * k - z) * pow(r, -1, ORDER)) % ORDER
private_key_2 = ((-s * k - z) * pow(r, -1, ORDER)) % ORDER
print(hex(private_key_1))
print(hex(private_key_2))
The private keys calculated using the above method are shown in the table below:
1
b7010000ffd8ffe000104a46494600010101004800480000ffdb004300432e32
2
3a322a433a363a4b47434f64a66c645c5c64cc929a79a6f1d4fefaedd4e9e5ff
3
ffffffffffffffe5e9ffffffffffffffffffffffffffffffffffffffffffc000
4
0b08002b002b01011100ffc40019000002030100000000000000000000000004
5
0500020301ffc400251000020202010305010101000000000000010200030411
6
122122611331415171a13281ffda0008010100003f0036cb16a42ee740459767
7
5961210f05f1ef072ccdd4927ccbd7916d67b5cfe1ea231c5cb5bfb5bb5febee
8
131567dc6cb8a03da9d3fec1d38f31cf6577d75192e3d4943147e22d0002df13
9
0cda0af17441e985036208ac558329d11ec639a6d16d4afd06c44cc49624fb93
10
222f37551f27519e5ad6ca9535a2bf91d272c031b04a6cbec6b7fb164d52c655
11
0013a9cc9acd77baf9d8fc9b615952baab5659cb746fa84e45156439736f1e3d
12
a7e84adf6555627a48e1ceb43aee2e8cb1f114d085fdc8dcbe6637aebb5ff63d
13
bcc59df53fcab2ff00258dced5942760b723fb338561e21b583b8d20fec6924c
14
eda6bb477a03e62ab5155f4074dc370e8a8af22809f30c927fffd90000000000
15
Not disclosed
Once you have obtained all the private keys, simply concatenate them together and remove some bytes from both ends to get the following string.
ffd8ffe000104a46494600010101004800480000ffdb004300432e323a322a433a363a4b47434f64a66c645c5c64cc929a79a6f1d4fefaedd4e9e5ffffffffffffffffe5e9ffffffffffffffffffffffffffffffffffffffffffc0000b08002b002b01011100ffc400190000020301000000000000000000000000040500020301ffc400251000020202010305010101000000000000010200030411122122611331415171a13281ffda0008010100003f0036cb16a42ee7404597675961210f05f1ef072ccdd4927ccbd7916d67b5cfe1ea231c5cb5bfb5bb5febee131567dc6cb8a03da9d3fec1d38f31cf6577d75192e3d4943147e22d0002df130cda0af17441e985036208ac558329d11ec639a6d16d4afd06c44cc49624fb93222f37551f27519e5ad6ca9535a2bf91d272c031b04a6cbec6b7fb164d52c6550013a9cc9acd77baf9d8fc9b615952baab5659cb746fa84e45156439736f1e3da7e84adf6555627a48e1ceb43aee2e8cb1f114d085fdc8dcbe6637aebb5ff63dbcc59df53fcab2ff00258dced5942760b723fb338561e21b583b8d20fec6924ceda6bb477a03e62ab5155f4074dc370e8a8af22809f30c927fffd9
This 439-byte hexadecimal data can be converted into a JPG file. This results in the following unstoppable image:

免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。




