Gonka Algorithm Series Part Three: Detailed Explanation of Computational Challenges and Anti-Cheat Mechanisms

Introduction: The Core Mechanism of Gonka PoW 2.0

The core idea of Gonka PoW 2.0 is to transform traditional proof of work into meaningful AI computation tasks. This article will delve into its two main core mechanisms: the generation of computational challenges and the anti-cheating verification system, demonstrating how this innovative consensus mechanism establishes a reliable anti-cheating guarantee while ensuring the usefulness of computations.

The entire process can be summarized in the following diagram: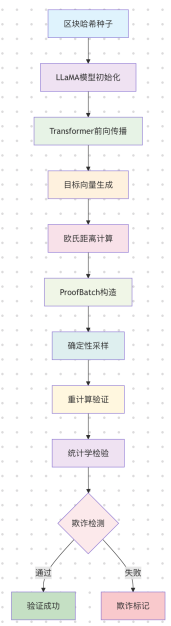

1. Generation Mechanism of Computational Challenges

Computational challenges are at the heart of Gonka PoW 2.0, transforming traditional proof of work into meaningful AI computation tasks. Unlike traditional PoW, Gonka's computational challenges are not simple hash calculations but a complete deep learning inference process, ensuring network security while producing usable computational results.

1.1 Unified Management of the Seed System

All computational processes are driven by a unified seed, ensuring that all nodes in the network perform the same computational tasks. This design guarantees the reproducibility and fairness of computations, as each node must execute the same computational task to obtain valid results.

Data Source: mlnode/packages/pow/src/pow/compute/compute.py#L217-L225

Key elements of the seed system include:

- Block Hash: As the main seed, it ensures the consistency of computational tasks.

- Public Key: Identifies the identity of the computing node.

- Block Height: Ensures time synchronization.

- Parameter Configuration: Controls model architecture and computational complexity.

1.2 Deterministic Initialization of LLaMA Model Weights

Each computational task starts with a unified LLaMA model architecture, with weights deterministically initialized through the block hash. This design ensures that all nodes use the same model structure and initial weights, thereby guaranteeing the consistency of computational results.

Data Source: mlnode/packages/pow/src/pow/models/llama31.py#L32-L51

Mathematical principles of weight initialization:

- Normal Distribution: N(0, 0.02²) - Small variance ensures gradient stability.

- Deterministic: The same block hash produces the same weights.

- Memory Efficiency: Supports float16 precision to reduce memory usage.

1.3 Target Vector Generation and Distance Calculation

Target vectors are uniformly distributed on a high-dimensional unit sphere, which is key to the fairness of computational challenges. By generating uniformly distributed target vectors in high-dimensional space, the randomness and fairness of computational challenges are ensured.

Data Source: mlnode/packages/pow/src/pow/random.py#L165-L177

In the 4096-dimensional vocabulary space, spherical geometry has the following characteristics:

- Unit Length: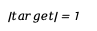

- Angle Distribution: The angle between any two random vectors tends to 90°.

- Concentration Phenomenon: Most mass is distributed near the surface of the sphere.

Mathematical principles of spherical uniform distribution:

In n-dimensional space, uniform distribution on the unit sphere can be generated as follows:

First, generate n independent standard normal distribution random variables:
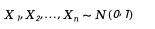
Then normalize:

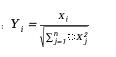
This method ensures that the generated vectors are uniformly distributed on the sphere, mathematically expressed as:

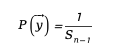
where 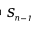is the surface area of the (n-1)-dimensional sphere.

Distance calculation is a key step in verifying computational results, measuring the effectiveness of computations by calculating the Euclidean distance between the model output and the target vector:

Data Source: Based on the processing logic in mlnode/packages/pow/src/pow/compute/compute.py

Steps for distance calculation:

Permutation Application: Rearrange output dimensions according to the permutation seed.
Vector Normalization: Ensure all output vectors are on the unit sphere.
Distance Calculation: Calculate the Euclidean distance to the target vector.
Batch Packaging: Package the results into a ProofBatch data structure.

2. Anti-Cheating Verification Mechanism

To ensure the fairness and security of computational challenges, the system has designed a sophisticated anti-cheating verification system. This mechanism verifies the authenticity of computations through deterministic sampling and statistical testing, preventing malicious nodes from gaining improper benefits through cheating.

2.1 ProofBatch Data Structure

Computational results are encapsulated in a ProofBatch data structure, which is the core carrier of the verification process. ProofBatch contains the identity information of the computing nodes, timestamps, and computational results, providing the necessary data foundation for subsequent verification.

Data Source: mlnode/packages/pow/src/pow/data.py#L8-L25

Characteristics of the ProofBatch data structure:

- Identity Identification: public_key uniquely identifies the computing node.

- Blockchain Binding: blockhash and blockheight ensure time synchronization.

- Computational Results: nonces and dist record all attempts and their distance values.

- Sub-batch Support: Supports extraction of successful computations that meet the threshold.

2.2 Deterministic Sampling Mechanism

To improve verification efficiency, the system employs a deterministic sampling mechanism, verifying only a portion of computational results rather than all. This design ensures the effectiveness of verification while significantly reducing verification costs.

The verification sampling rate of Gonka is uniformly managed through on-chain parameters, ensuring consistency across the network:

Data Source: inference-chain/proto/inference/inference/params.proto#L75-L78

Data Source: inference-chain/x/inference/types/params.go#L129-L133

Based on the seed system, the sampling process is completely deterministic, ensuring the fairness of verification. By using the SHA-256 hash function and information such as the verifier's public key, block hash, and block height to generate seeds, it ensures that all verifiers use the same sampling strategy:

Data Source: decentralized-api/mlnodeclient/poc.go#L175-L201

Advantages of Deterministic Sampling:

- Fairness: All verifiers use the same sampling strategy.

- Efficiency: Only a portion of the data is verified, reducing verification costs.

- Security: It is difficult to predict the sampled data, preventing cheating.

2.3 Statistical Fraud Detection

The system uses a binomial distribution test to detect fraudulent behavior, determining whether computing nodes are honest through statistical methods. This approach sets an expected error rate based on hardware precision and computational complexity, and detects anomalies through statistical testing.

Data Source: mlnode/packages/pow/src/pow/data.py#L7

The setting of the expected error rate considers the following factors:

- Floating Point Precision: Differences in floating-point computation precision across different hardware.

- Parallel Computing: Numerical accumulation errors caused by GPU parallelization.

- Randomness: Minor differences in model weight initialization.

- System Differences: Variations in computational behavior across different operating systems and drivers.

Data Source: mlnode/packages/pow/src/pow/data.py#L174-L204

Conclusion: Building a Secure and Reliable AI Computing Network

Gonka PoW 2.0 successfully combines the security needs of blockchain with the practical value of AI computing through carefully designed computational challenges and anti-cheating verification mechanisms. The computational challenges ensure the meaningfulness of the work, while the anti-cheating mechanisms guarantee the fairness and security of the network.

This design not only validates the technical feasibility of "meaningful mining" but also establishes a new standard for distributed AI computing: computations must be both secure and useful, verifiable and efficient.

By integrating statistics, cryptography, and distributed system design, Gonka PoW 2.0 successfully establishes a reliable anti-cheating mechanism while ensuring the usefulness of computations, providing a solid security foundation for the technical route of "meaningful mining."

Note: This article is based on the actual code implementation and design documents of the Gonka project, and all technical analyses and configuration parameters are derived from the project's official code repository.

About Gonka.ai

Gonka is a decentralized network aimed at providing efficient AI computing power, designed to maximize the utilization of global GPU computing resources to complete meaningful AI workloads. By eliminating centralized gatekeepers, Gonka offers developers and researchers permissionless access to computing resources while rewarding all participants with its native token GNK.

Gonka is incubated by the American AI developer Product Science Inc., founded by industry veterans from Web 2, including former Snap Inc. core product director Libermans siblings. In 2023, the company successfully raised $18 million, with investors including OpenAI investor Coatue Management, Solana investor Slow Ventures, K 5, Insight and Benchmark partners, among others. Early contributors to the project include well-known leading companies in the Web 2-Web 3 space such as 6 blocks, Hard Yaka, Gcore, and Bitfury.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。