Title: Adaptor Signatures and Its Application to Cross-Chain Atomic Swaps

Original article link: https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

Authors: mutourend, lynndell

1. Introduction

With the rapid development of Bitcoin Layer2 expansion solutions, the frequency of cross-chain asset transfers between Bitcoin and its Layer2 corresponding networks has significantly increased. This trend is driven by the higher scalability, lower transaction fees, and higher throughput provided by Layer2 technologies (such as Bitlayer). These advancements have facilitated more efficient and economical transactions, thereby promoting wider adoption and integration of Bitcoin in various applications. As a result, interoperability between Bitcoin and Layer2 networks is becoming a key component of the cryptocurrency ecosystem, driving innovation and providing users with a more diverse and powerful set of financial tools.

As shown in Table 1, there are three typical approaches to cross-chain transactions between Bitcoin and Layer2, namely centralized cross-chain transactions, BitVM cross-chain bridges, and cross-chain atomic swaps. These three technologies differ in terms of trust assumptions, security, convenience, transaction limits, and can meet different application requirements.

Table 1. Comparison of Cross-Chain Transaction Technologies

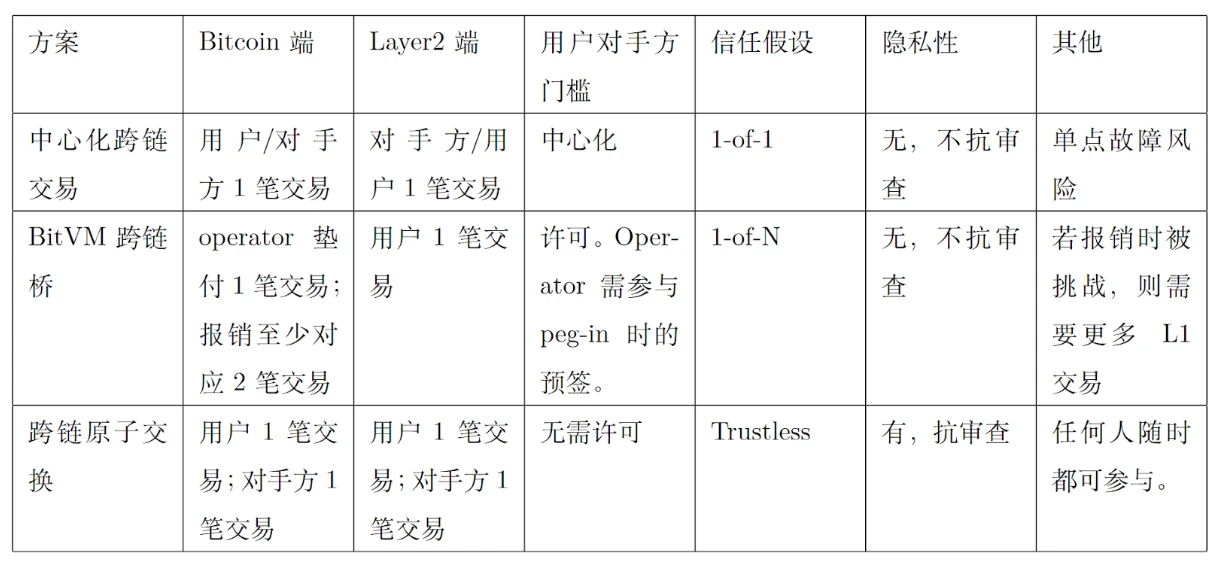
Centralized Cross-Chain Transactions: In this approach, users first send Bitcoin to a centralized institution (such as a project party or exchange), and the centralized institution then transfers equivalent assets on the Layer2 network to the user's specified address, completing the cross-chain asset transfer. The advantage of this technology lies in its speed and relatively easy matching process, as centralized institutions can quickly confirm and process transactions. However, the security of this method relies entirely on the reliability and reputation of the centralized institution. If the centralized institution encounters technical failures, malicious attacks, or defaults, users' funds face higher risks. Additionally, centralized cross-chain transactions may also compromise user privacy, so users need to carefully consider this method when choosing it. Therefore, while its convenience and efficiency provide great convenience for users, security and trust are the main challenges faced by centralized cross-chain transactions.

BitVM Cross-Chain Bridges: This technology is relatively complex. In the Peg-in phase, users send Bitcoin to a multi-signature address controlled by the BitVM alliance, achieving Bitcoin locking. Corresponding tokens are then minted on Layer2, and Layer2 transactions and applications are carried out using these tokens. When users destroy Layer2 tokens, the Operator provides the corresponding payment. Subsequently, the Operator reimburses the corresponding amount of Bitcoin to the multi-signature pool controlled by the BitVM alliance. To prevent malicious behavior by the Operator, the reimbursement process adopts an optimistic challenge mechanism, where any third party can initiate a challenge to defeat malicious behavior. This technology introduces an optimistic challenge mechanism, making the technology relatively complex. In addition, the optimistic challenge mechanism involves a large number of challenge and response transactions, resulting in higher transaction fees. Therefore, BitVM cross-chain bridges are only suitable for large transactions, similar to U's issuance, resulting in lower usage frequency.

Cross-Chain Atomic Swaps: Atomic swaps are contracts that enable decentralized cryptocurrency transactions. In this case, "atomic" means that a change in ownership of one asset actually means a change in ownership of another asset. This concept was first proposed by TierNolan on the Bitcointalk forum in 2013. For 4 years, atomic swaps remained in the theoretical domain. It wasn't until 2017 that Decred and Litecoin became the first blockchain systems to successfully complete atomic swaps. Atomic swaps must involve two parties, and any third party cannot interrupt or interfere with the exchange process. This means that the technology is decentralized, uncensored, provides good privacy protection, and enables high-frequency cross-chain transactions, making it widely applicable in decentralized exchanges. Currently, cross-chain atomic swaps require 4 transactions, and some schemes attempt to compress the number of transactions to 2, but this increases the real-time online requirements for the exchanging parties, etc. Finally, cross-chain atomic swap technology mainly includes Hashed Time Lock Contracts (HTLC) and adaptor signatures.

Cross-Chain Atomic Swaps Based on Hashed Time Lock Contracts (HTLC): The first project to successfully implement cross-chain atomic swaps was Decred, which used "hash locks" and "time locks" to achieve the atomic swaps proposed by TierNolan using on-chain scripts (or smart contracts). HTLC allows two users to conduct time-bound cryptocurrency transactions, where the recipient must submit cryptographic proof ("secret") to the contract within a specified time (determined by block count or block height), otherwise the funds will be returned to the sender. If the recipient confirms the payment, the transaction is successful. Therefore, both blockchains involved in the exchange must have "hash locks" and "time locks" functionality.

Although HTLC atomic swaps represent a significant breakthrough in the field of decentralized exchange technology, they have the following issues. These atomic swap transactions and the data associated with them are conducted on-chain, leading to privacy leaks for users. In other words, each exchange results in the appearance of the same hash value on both blockchains, separated by only a few blocks. This means that observers can link the currencies involved in the exchange, finding the same hash value in blocks close to each other (TimeStamp-wise). When tracking cross-chain currencies, it is easy to determine their origin. Although this analysis does not reveal any related identity data, third parties can easily infer the identities of the participants involved.

Cross-Chain Atomic Swaps Based on Adaptor Signatures: The second type of exchange provided by BasicSwap is called "adaptor signature" atomic swaps, based on a paper titled "Bitcoin–Monero Cross-chain Atomic Swap" published by Monero developer Joël Gugger in 2020. This paper can be considered an implementation of Lloyd Fournier's 2019 paper "One-Time Verifiably Encrypted Signatures, A.K.A. Adaptor Signatures." Adaptor signatures are an additional signature that, when combined with the initial signature, reveals secret data, enabling both parties to simultaneously disclose two pieces of data to each other, and are a key component of the scriptless protocol that makes Monero atomic swaps possible.

Compared to HTLC atomic swaps, adaptor signature atomic swaps have three advantages: first, the adaptor signature exchange scheme replaces the on-chain scripts relied upon by "secret hash" exchanges, including time locks and hash locks. In other words, the secret and secret hash in HTLC exchanges do not have a direct correspondence in adaptor signature exchanges. Therefore, it is referred to as "scriptless scripts" in the Bitcoin research community. Additionally, since it does not involve such scripts, the on-chain space is reduced, making adaptor signature atomic swaps lighter and less costly. Finally, HTLC requires the use of the same hash value on each chain, while transactions involved in adaptor signature atomic swaps cannot be linked, achieving privacy protection.

This article first introduces the principles of Schnorr/ECDSA adaptor signatures and cross-chain atomic swaps. Then, it analyzes the random number security issues in adaptor signatures and the system heterogeneity and algorithm heterogeneity issues in cross-chain scenarios, and provides solutions. Finally, it extends the application of adaptor signatures to achieve non-interactive digital asset custody.

2. Adaptor Signatures and Cross-Chain Atomic Swaps

2.1 Schnorr Adaptor Signatures and Atomic Swaps

2.2 ECDSA Adaptor Signatures and Atomic Swaps

2.2.1 Zero-Knowledge Proof zk{v | Ṽ = v ᐧ G, V = v ᐧ Y}

3. Security Issues and Solutions

3.1 Random Number Issues and Solutions

3.1.1 Random Number Leakage Issue

Pre-signatures of Schnorr/ECDSA adaptor signatures commit to the random number $r$, represented as $Ȓ = r ᐧ G$. Additionally, zero-knowledge proofs commit to the random number $v$, represented as $Ṽ=v ᐧ G,V=v ᐧ Y$. Leakage of the random number would lead to private key exposure.

Specifically, in the Schnorr protocol, if the random number $r$ leaks, the private key $x$ can be calculated from the equation

$ŝ = r + c x.$

Similarly, in the ECDSA protocol, if the random number $r$ leaks, the private key $x$ can be calculated from the equation

$ŝ = r^{-1}(hash(m)+R_x x).$

Finally, in the zero-knowledge proof protocol, if the random number $v$ leaks, the random number $r$ can be calculated from the equation

$z := v + c r.$

This would further lead to the calculation of the private key $x$ based on the random number $r$. Therefore, the random number should be immediately deleted after use.

3.1.2 Random Number Reuse Issue

If the same random number is used for any two cross-chain transactions, it would lead to private key exposure. Specifically, in the Schnorr protocol, if the same random number $r$ is used, the following system of equations has only $r$ and $x$ as unknowns

$ŝ_1 =r + c_1 x, $

$ ŝ_2 = r + c_2 x. $

Similarly, in the ECDSA adaptor signature protocol, if the same random number $r$ is used, the following system of equations has only $r$ and $x$ as unknowns

$ ŝ_1 = r^{-1}(hash(m_1)+R_x x),$

$ ŝ_2 = r^{-1}(hash(m_2)+R_x x).$

Finally, in the zero-knowledge proof protocol, if the same random number $v$ is used, the following system of equations has only $v$ and $r$ as unknowns

$z_1 = v+c_1 r, $

$ z_2 = v+c_2 r. $

This would lead to the calculation of the random number $r$, and further solving the system of equations to obtain the private key $x$.

Similarly, different users using the same random number would also lead to private key exposure. In other words, two users using the same random number can solve the system of equations to obtain each other's private keys. Therefore, the use of RFC 6979 is necessary to address the random number reuse issue.

3.1.3 Solution: RFC 6979

RFC 6979 specifies a method for generating deterministic digital signatures using DSA and ECDSA, addressing security issues related to the generation of the random value $k$. Traditional DSA and ECDSA signatures rely on a randomly generated random number $k$ for each signing operation. If this random number is reused or generated improperly, it could compromise the security of the private key. RFC 6979 eliminates the need for generating random numbers by deterministically deriving $k$ from the private key and the message to be signed. This ensures that the signature is always the same when the same message is signed with the same private key, enhancing reproducibility and predictability. Specifically, the deterministic $k$ is generated using HMAC, involving the hash function (e.g., SHA256) to compute the hash value of the private key, message, and a counter,

$k = SHA256(sk, msg, counter).$

This equation ensures that $k$ is unique for each message, has reproducibility for the same input, and reduces the risk of private key exposure associated with a weak or compromised random number generator. Therefore, RFC 6979 provides a robust framework for deterministic digital signatures using DSA and ECDSA, addressing significant security issues related to random number generation and enhancing the reliability and predictability of digital signatures. This makes it a valuable standard for applications requiring high security and strict operational requirements. Schnorr/ECDSA signatures have random number flaws and need to use RFC 6979 for prevention. Therefore, adaptor signatures based on Schnorr/ECDSA also face these issues and need to adhere to the RFC 6979 specification to address them.

3.2 Cross-Chain Scenario Issues and Solutions

3.2.1 UTXO and Account Model System Heterogeneity Issue and Solution

As shown in Figure 1, Bitcoin uses the UTXO model and implements native ECDSA signatures based on the Secp256k1 curve. Bitlayer is an EVM-compatible Bitcoin L2 chain, using the Secp256k1 curve and supporting native ECDSA signatures. Adaptor signatures implement the logic required for BTC exchanges, while the Bitlayer exchange counterpart is supported by the powerful capabilities of Ethereum smart contracts.

Cross-chain atomic swaps based on adaptor signatures, or at least designed for the semi-scriptless adaptor signature scheme for the ECDSA curve, are incompatible with Ethereum. This is because Ethereum uses an account model, not a UTXO model. Specifically, for cross-chain atomic swaps based on adaptor signatures, the refund transaction must be pre-signed. However, in the Ethereum system, a transaction cannot be pre-signed without knowing the nonce. Therefore, one party can send a transaction between pre-signing and transaction execution, rendering the pre-signed transaction invalid (since the nonce has been used and cannot be reused).

Additionally, from a privacy perspective, this means that the anonymity of Bitlayer swaps is better than HTLC (both parties can find the contract). However, because one party needs to have a public contract, the anonymity of Bitlayer swaps is lower than the anonymity of adaptor signatures. For the party without the contract, the swap transaction looks the same as any other transaction. However, for the party with the EVM contract, the transaction is clearly for asset swaps. Even with complex chain analysis tools, it is not possible to trace it back to the other chain.

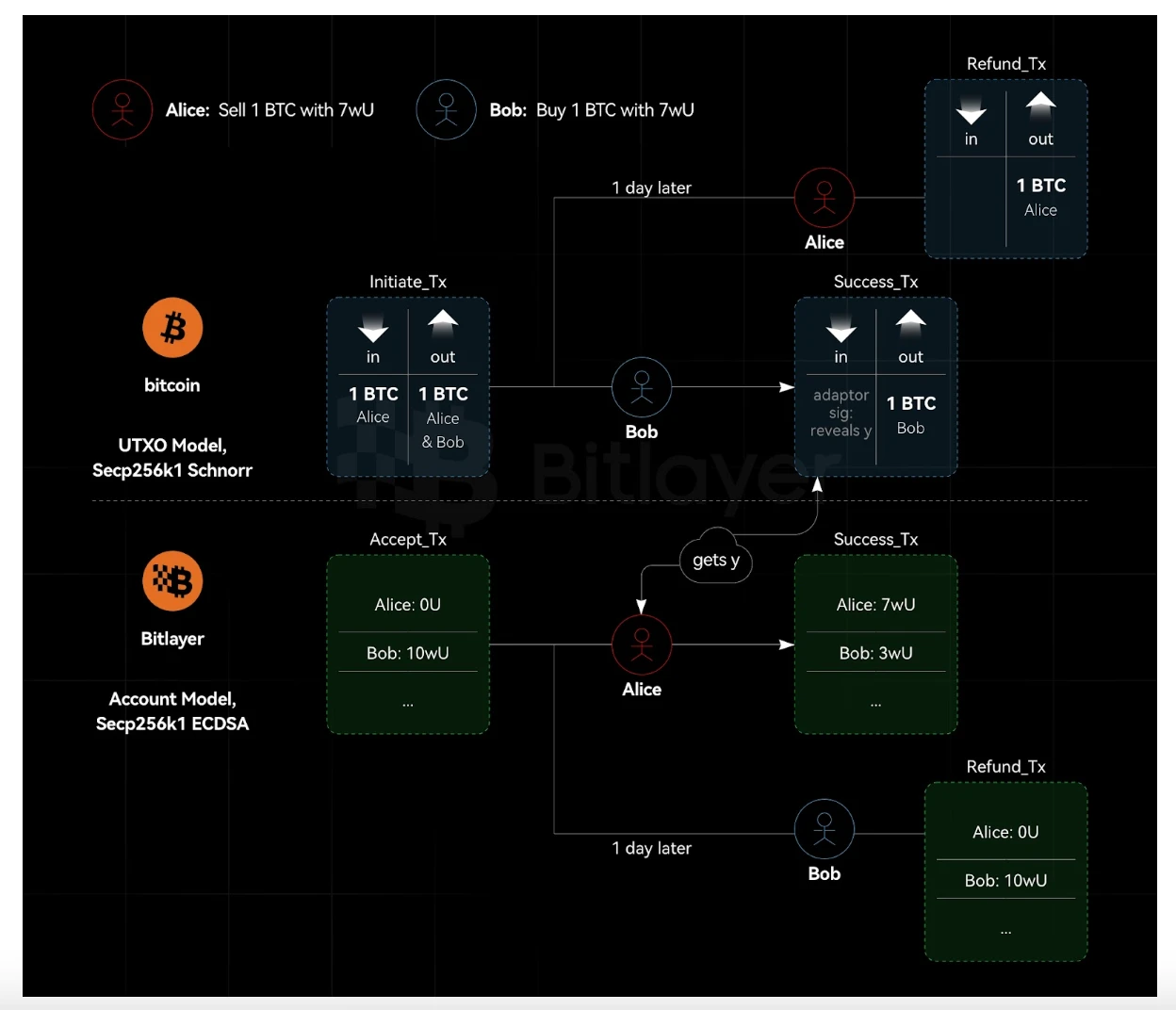
Figure 1. Heterogeneity of UTXO and Account Model Systems in Cross-Chain Atomic Swaps

Bitlayer currently supports native ECDSA signatures and can also implement Schnorr signature verification through smart contracts. If native Bitlayer transactions are used, the refund transaction for atomic swaps cannot be pre-signed; smart contract transactions on Bitlayer are required to achieve atomic swaps. However, this process sacrifices privacy, as transactions involved in atomic swaps in the Bitlayer system are traceable, but cannot be traced back to transactions in the BTC system. Dapp applications similar to Tornado Cash can be designed on the Bitlayer side to provide privacy services for Bitlayer transactions involved in atomic swaps.

3.2.2 Security of Adaptor Signatures with Same Curve but Different Algorithms

As shown in Figure 2, assuming both Bitcoin and Bitlayer use the Secp256k1 curve, but Bitcoin uses Schnorr signatures while Bitlayer uses ECDSA. In this case, adaptor signatures based on Schnorr and ECDSA are provably secure. If given ECDSA and Schnorr signature oracles, and a simulator S can break ECDSA, then given only the ECDSA signature oracle, a simulator S can break ECDSA. However, ECDSA is secure. Similarly, if given ECDSA and Schnorr signature oracles, and a simulator S can break Schnorr signatures, then given only the ECDSA signature oracle, a simulator S can break Schnorr signatures. However, Schnorr signatures are secure. Therefore, in a cross-chain scenario, adaptor signatures using the same curve but different signature algorithms are secure. In other words, adaptor signatures allow one side to use ECDSA while the other side uses Schnorr signatures.

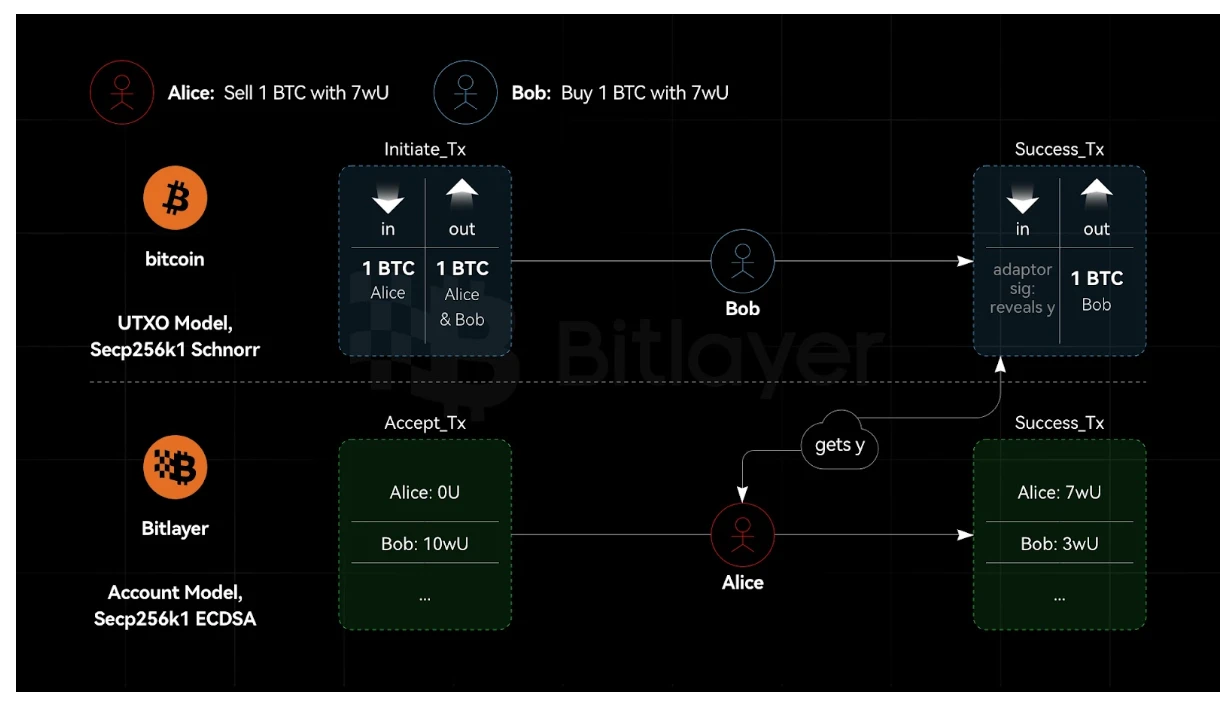
Figure 2. Adaptor Signatures with Same Curve but Different Algorithms

3.2.3 Insecurity of Adaptor Signatures with Different Curves

If Bitcoin uses the Secp256k1 curve and ECDSA signatures, while Bitlayer uses the ed25519 curve and Schnorr signatures, adaptor signatures cannot be used. Due to the different curves, the orders of the elliptic curve groups are different, i.e., the modulus coefficients are different. When Bob adapts $y$ to the ECDSA signature in the Bitcoin system, i.e., computes $s:= ŝ+y$, the possible values of $y$ belong to the scalar space of the Secp256k1 elliptic curve group. Subsequently, Alice needs to use $y$ to perform Schnorr signatures on the ed25519 elliptic curve group in Bitlayer. However, the ed25519 curve has a cofactor of 8, and the modulus coefficient is not equal to that of the Secp256k1 elliptic curve group. Therefore, using $y$ for Schnorr signatures on the ed25519 curve is insecure.

4. Digital Asset Custody Applications

Digital asset custody involves three parties: the buyer Alice, the seller Bob, and the custodian. Using adaptor signatures can achieve non-interactive threshold digital asset custody and instantiate a subset of threshold spending policies without the need for interaction. This subset consists of two types of participants: participants involved in the initialization and participants not involved in the initialization, the latter being the custodian. The custodian cannot sign arbitrary transactions but only sends secrets to one of the supported parties.

On one hand, the custodian can only choose from a few fixed settlement transactions and cannot sign new transactions with either of the other parties. Therefore, this secret release mechanism makes the flexibility of non-interactive threshold custody less than that of threshold Schnorr signatures. On the other hand, a 2-of-3 spending policy can be set up using threshold Schnorr signatures. However, the threshold Schnorr signature protocol requires three-party execution for decentralized key generation. Therefore, asset custody protocols based on adaptor signatures have non-interactive advantages.

4.1 Non-Interactive Asset Custody Based on Adaptor Signatures

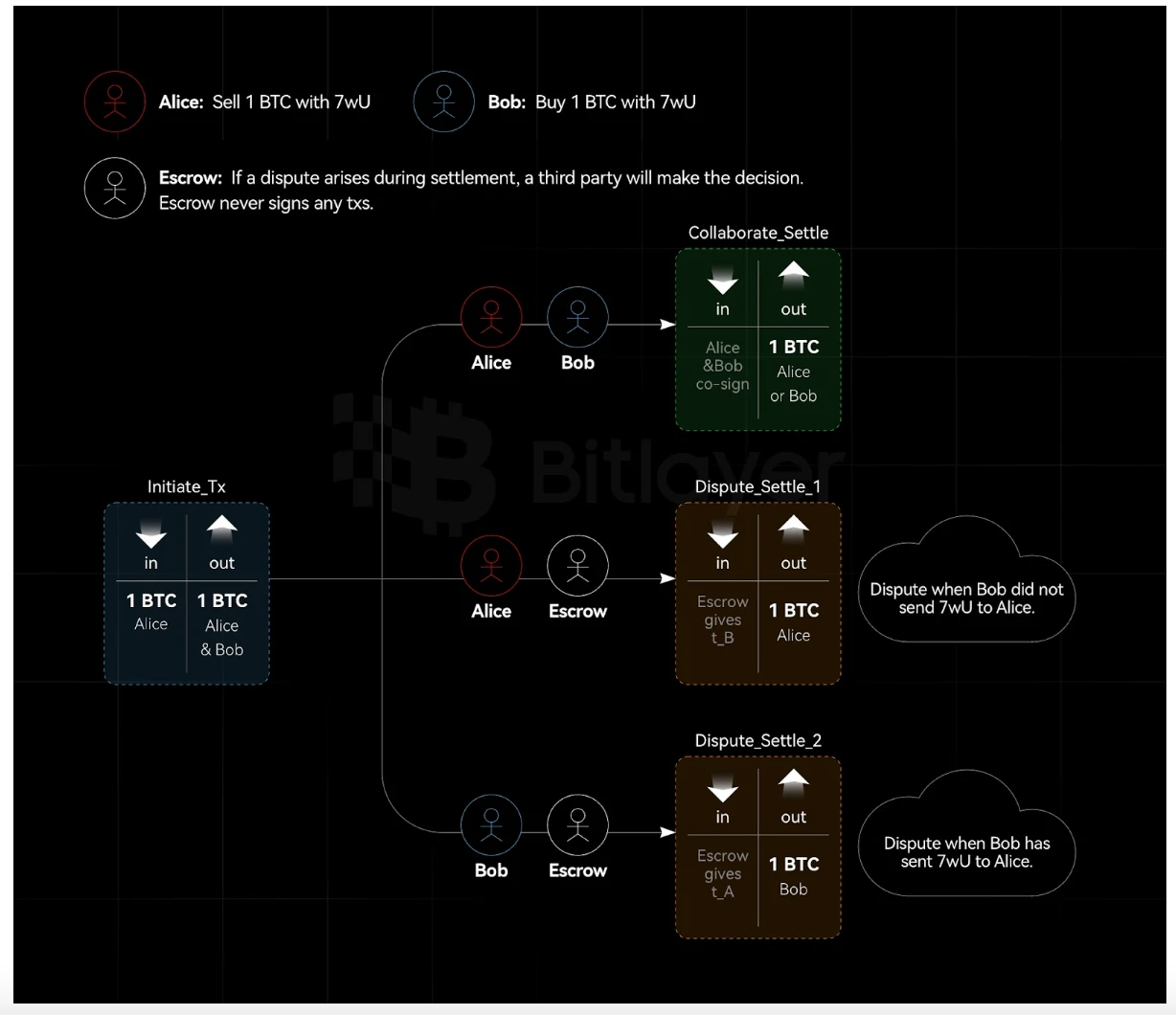
Figure 3. Non-Interactive Asset Custody Based on Adaptor Signatures

As shown in Figure 3, Alice and Bob want to create a 2-of-3 transaction output with a hidden policy, including a custodian. Depending on condition $c$, Alice or Bob can spend the transaction output. If there is a dispute between Alice and Bob, the custodian (public key $E$, private key $e$) decides which party, Alice or Bob, receives the assets.

• Create an unsigned funding transaction to send BTC to a 2-of-2 MuSig output between Alice and Bob.

• Alice chooses a random value $t_A$ and sends an adaptor Schnorr pre-signature $(\hat{R}_A,\hat{s}_A)$ of a transaction with the adaptor as $t_A ᐧ G$ to Bob, which is to send the funding output to Bob. Alice also sends a ciphertext to Bob containing the secret $t_A$ and adjusts the custodian public key $E$ to $E_c = E + hash(E, c)G$ for verifiable encryption $C = Enc(E_c, t_A)$. Upon receiving Alice's pre-signature, Bob adds his own signature, which does not satisfy the 2-of-2 MuSig, and therefore cannot spend the funding output. Only when Bob knows $t_A$ (provided by the custodian), or Alice signs the complete signature separately and sends it to Bob, can the funding output be spent.

• Correspondingly, Bob repeats step (2) based on his adaptor secret $t_B$. At this point, the transaction signed by Bob is to send the funding output to Alice.

• Alice and Bob both verify the validity of the received ciphertext, confirming that the ciphertext is an encryption of the secret for $E_c$, and sign and broadcast the funding transaction. Verifiable encryption allows the custodian to not participate in the setup phase and does not require the public contract $c$ to be disclosed.

• In case of a dispute, Alice and Bob can send the ciphertext and condition $c$ to the custodian, who can make a judgment based on the actual situation, and use the adjusted private key $e+hash(E, c)$ to decrypt and send $t_A/t_B$ to Bob/Alice.

If there is no dispute, Alice and Bob can spend the 2-of-2 MuSig output as they wish. In case of a dispute, either party can contact the custodian and request their adaptor secret $t_A$ or $t_B$. Therefore, with the help of the custodian, one party can complete the adaptor signature and broadcast the settlement transaction.

4.2 Verifiable Encryption

Classic verifiable encryption schemes based on discrete logarithms (Practical Verifiable Encryption and Decryption of Discrete Logarithms) cannot be used for Secp256k1 adaptors, as they only support verification of specially structured groups.

Currently, there are two promising ways to achieve verifiable encryption based on Secp256k1 discrete logarithms, namely Purify and Juggling.

Purify was originally proposed to create a MuSig protocol with deterministic nonces (DN), requiring each signer to use zero-knowledge proofs to demonstrate that their nonce is the result of correctly applying a pseudo-random function (PRF) to the public key and the message. The Purify PRF can be efficiently implemented in the arithmetic circuit of Bulletproofs zero-knowledge protocol, used to create a verifiable encryption scheme based on discrete logarithms on Secp256k1. In other words, verifiable encryption is achieved using zkSnark.

Juggling encryption involves four steps: (1) splitting the discrete logarithm $x$ into multiple fragments of length $l$, such that $x = \sum _k 2^{(k-1)l} x_k$; (2) using the public key $Y$ to perform ElGamal encryption of the fragment $x_k ᐧ G$, resulting in $\{ D_k, E_k\} = \{ x_k ᐧ G + r_k ᐧ Y, r_k ᐧ G \}$; (3) creating a range proof for each $x_k ᐧ G$, proving that $D_k$ is a Pedersen commitment to $x_k ᐧ G + r_k ᐧ Y$, and its value is less than $2^l$; (4) using the sigma protocol to prove that $\{sum D_k, sum E_k\}$ is a correct encryption of $x_k ᐧ G$.

During the decryption process, each $x_k ᐧ G$ is decrypted from $\{D_k, E_k\}$, and then an exhaustive search is performed to find $x_k$ (with a range of $[0, 2^l)$).

Purify requires the execution of a PRF within Bulletproofs, making it relatively complex, while Juggling is theoretically simpler. Additionally, the difference between the two in terms of proof size, proof duration, and verification duration is minimal.

5. Summary

This article provides a detailed description of the principles of Schnorr/ECDSA adaptor signatures and cross-chain atomic swaps. It thoroughly analyzes the issues of random number leakage and repetition in adaptor signatures, and proposes the use of RFC 6979 to address these issues. Furthermore, it analyzes in detail the considerations for cross-chain applications, not only in terms of the differences between the UTXO model and the account model of blockchains, but also in terms of whether adaptor signatures support different algorithms and different curves. Finally, it extends the application of adaptor signatures to achieve non-interactive digital asset custody, and briefly introduces the cryptographic primitive involved—verifiable encryption.

References

• Gugger J. Bitcoin-monero cross-chain atomic swap[J]. Cryptology ePrint Archive, 2020.

• Fournier L. One-time verifiably encrypted signatures aka adaptor signatures[J]. 2019, 2019.

• https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

• Pornin T. Deterministic usage of the digital signature algorithm (DSA) and elliptic curve digital signature algorithm (ECDSA)[R]. 2013.

• Komlo C, Goldberg I. FROST: flexible round-optimized Schnorr threshold signatures[C]//Selected Areas in Cryptography: 27th International Conference, Halifax, NS, Canada (Virtual Event), October 21-23, 2020, Revised Selected Papers 27. Springer International Publishing, 2021: 34-65.

• https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md

• https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/

• Camenisch J, Shoup V. Practical verifiable encryption and decryption of discrete logarithms[C]//Annual International Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003: 126-144.

• Nick J, Ruffing T, Seurin Y, et al. MuSig-DN: Schnorr multi-signatures with verifiably deterministic nonces[C]//Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. 2020: 1717-1731.

• Shlomovits O, Leiba O. Jugglingswap: scriptless atomic cross-chain swaps[J]. arXiv preprint arXiv:2007.14423, 2020.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。